题目内容
13.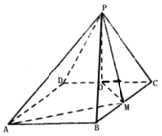 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 连接BD,OB,PB,则OM∥BD,∠PDB或其补角为异面直线OM与PD所成角,△PBD中,由余弦定理可得cos∠PDB.
解答  解:连接BD,OB,PB,则OM∥BD,∴∠PDB或其补角为异面直线OM与PD所成角.
解:连接BD,OB,PB,则OM∥BD,∴∠PDB或其补角为异面直线OM与PD所成角.
由条件PO⊥平面ABCD,则OB=3,PO=$\sqrt{3}$,BD=2$\sqrt{3}$,PB=2$\sqrt{3}$,
△PBD中,由余弦定理可得cos∠PDB=$\frac{4+12-12}{2•2•2\sqrt{3}}$=$\frac{\sqrt{3}}{6}$,
故选:C.
点评 本题考查异面直线OM与PD所成角,考查余弦定理的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)=$\frac{1}{e}•{e^x}+\frac{a}{2}{x^2}$-(a+1)x+a(a>0),其中e为自然对数的底数.若函数y=f(x)与y=f[f(x)]有相同的值域,则实数a的最大值为( )
| A. | e | B. | 2 | C. | 1 | D. | $\frac{e}{2}$ |
5.已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{{\sqrt{2}}}{2}$,同时椭圆C上存在一点与右焦点关于直线x+y-1=0对称,则椭圆C的方程为( )
| A. | $\frac{{8{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$ | B. | $\frac{{9{x^2}}}{8}+\frac{{16{y^2}}}{9}=1$ | C. | $\frac{{8{x^2}}}{9}+\frac{{9{y^2}}}{16}=1$ | D. | $\frac{{9{x^2}}}{8}+\frac{{9{y^2}}}{16}=1$ |
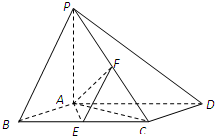 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,