题目内容
12.已知函数f(x)=|2x-a|-|x-1|.(1)当a=1时,求f(x)的最小值;
(2)存在x∈[0,2]时,使得不等式f(x)≤0成立,求实数a的取值范围.
分析 (1)当a=1时,f(x)=|2x-1|-|x-1|=$\left\{\begin{array}{l}{-x,x<\frac{1}{2}}\\{3x-2,\frac{1}{2}≤x≤1}\\{x,x>1}\end{array}\right.$,利用函数的单调性,即可求f(x)的最小值;
(2)不等式f(x)≤0,可化为(3x-a-1)(x-a+1)≤0,分类讨论,即可求实数a的取值范围.
解答 解:(1)当a=1时,f(x)=|2x-1|-|x-1|=$\left\{\begin{array}{l}{-x,x<\frac{1}{2}}\\{3x-2,\frac{1}{2}≤x≤1}\\{x,x>1}\end{array}\right.$.
∴f(x)在(-∞,$\frac{1}{2}$]上单调递减,在[$\frac{1}{2}$,+∞)上单调递增,
∴x=$\frac{1}{2}$时,f(x)取得最小值-$\frac{1}{2}$;
(2)不等式f(x)≤0,可化为(3x-a-1)(x-a+1)≤0.
a=2时,f(x)≤0,即x=1∈[0,2],符合题意;
a<2时,a-1<$\frac{a+1}{3}$,f(x)≤0的解集为[a-1,$\frac{a+1}{3}$],
∴[a-1,$\frac{a+1}{3}$]∩[0,2]≠∅,
∴a-1≤2且$\frac{a+1}{3}$≥0,
∴-1≤a<2;
a>2时,a-1>$\frac{a+1}{3}$,f(x)≤0的解集为[$\frac{a+1}{3}$,a-1],
∴[$\frac{a+1}{3}$,a-1]∩[0,2]≠∅,
∴a-1≥0且$\frac{a+1}{3}$≤2,
∴2<a≤5;
综上所述-1≤a≤5.
点评 本题考查绝对值不等式,考查函数的单调性与最值,考查分类讨论的数学思想,属于中档题.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
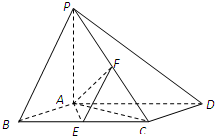 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,