题目内容
一个酒杯的轴截面是抛物线的一部分，它的方程是x2=2y（0≤y≤20）．在杯内放入一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r的范围是（ ）
| A、0＜r≤1 |
| B、0＜r＜1 |
| C、0＜r≤2 |
| D、0＜r＜2 |
考点：圆与圆锥曲线的综合
专题：圆锥曲线的定义、性质与方程
分析：设小球圆心（0，y0），抛物线上点（x，y），求得点到圆心距离平方的表达式，进而根据若r2最小值在（0，0）时取到，则小球触及杯底，需1-y0≥0，进而求得r的范围．
解答：
解：设小球圆心（0，y0），抛物线上点（x，y），则
点到圆心距离平方r2=x2+（y-y0）2=2y+（y-y0）2=r2+2（1-y0）y+y02．
若r2最小值在（0，0）时取到，则小球触及杯底，故此二次函数的对称轴位置应在y轴的左侧，
所以1-y0≥0，所以0＜y0≤1，
所以0＜r≤1．
故选A．
点到圆心距离平方r2=x2+（y-y0）2=2y+（y-y0）2=r2+2（1-y0）y+y02．
若r2最小值在（0，0）时取到，则小球触及杯底，故此二次函数的对称轴位置应在y轴的左侧，
所以1-y0≥0，所以0＜y0≤1，
所以0＜r≤1．
故选A．
点评：本题主要考查了抛物线的应用，考查了学生利用抛物线的基本知识解决实际问题的能力，考查二次函数的性质，属于中档题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
函数g（x）=lnx-
的零点所在区间是（ ）
| 1 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
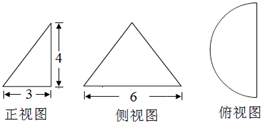某几何体的三视图如图所示（单位：cm），则其体积和表面积分别是（ ）| A、6πcm3和12（1+π）cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12（1+π）cm2 |
| D、12πcm3和12πcm2 |
若集合A={x∈R|y=lg（2-x）}，B={y∈R|y=2x-1，x∈A}，则∁R（A∩B）=（ ）
| A、R |
| B、（-∞，0]∪[2，+∞） |
| C、[2，+∞） |
| D、（-∞，0] |