题目内容
设在函数f(x)=xcosx-sinx的图象上的点(x0,y0)的切线斜率为k,若k=f′(x0),则函数k=f′(x0),x0∈[-π,π]的图象大致为( )
A、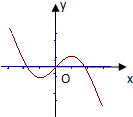 |
B、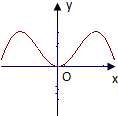 |
C、 |
D、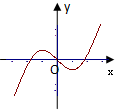 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,判断导函数的奇偶性,再结合导函数在[0,π]上的符号得答案.
解答:
解:由f(x)=xcosx-sinx,得
f′(x)=cosx-xsinx-cosx=-xsinx.
∴f′(x0)=-x0sinx0.
∵f′(-x0)=-(-x0)sin(-x0)=-x0sinx0=f′(x0),
∴函数k=f′(x0),x0∈[-π,π]为偶函数,
又当x0∈[0,π]时,k=f′(x0)<0,
∴函数k=f′(x0),x0∈[-π,π]的图象大致为选项C中的图象.
故选:C.
f′(x)=cosx-xsinx-cosx=-xsinx.
∴f′(x0)=-x0sinx0.
∵f′(-x0)=-(-x0)sin(-x0)=-x0sinx0=f′(x0),
∴函数k=f′(x0),x0∈[-π,π]为偶函数,
又当x0∈[0,π]时,k=f′(x0)<0,
∴函数k=f′(x0),x0∈[-π,π]的图象大致为选项C中的图象.
故选:C.
点评:本题考查了利用导数研究曲线上某点处的切线方程,函数在某点处的导数值就是对应曲线上该点处的切线的斜率,考查了函数奇偶性的判断方法,是中档题.

练习册系列答案
相关题目
如果函数f(x)=-
ln(x+1)的图象在x=1处的切线l过点(0,-
),并且l与圆x2+y2=
相离,则点(a,b)与圆x2+y2=10的位置关系是( )
| 2a |
| b |
| 1 |
| b |
| 1 |
| 10 |
| A、在圆内 | B、在圆外 |
| C、在圆上 | D、不能确定 |
下列各组函数相等的是( )
A、f(x)=
| ||||
B、f(x)=
| ||||
C、f(x)=2x+1 与g(x)=
| ||||
D、f(x)=|x2-1|与g(t)=
|
函数y=
sinx的导数为( )
| x |
A、y′=2
| ||||||
B、y′=
| ||||||
C、y′=
| ||||||
D、y′=
|
在△ABC中,∠B=
,AB=8,BC=5,则△ABC外接圆的面积为( )
| π |
| 3 |
A、
| ||
| B、16π | ||
C、
| ||
| D、15π |
函数y=4cos2x的图象可以由y=4sin(2x-
)的图象经过平移变换而得到,则这个平移变换是( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
在50和350之间,所有末位数字是1的整数之和是( )
| A、5880 | B、5684 |
| C、4877 | D、4566 |