题目内容
14．函数f（x）=（1-cosx）•sinx，x∈[-2π，2π]的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 利用排除法，即可求解．
解答 解：函数f（x）为奇函数，故排除B．
又x∈（0，π）时，f（x）＞0，故排除D．
又f（$\frac{2π}{3}$）=$\frac{3\sqrt{3}}{4}$＞1，故排除A．
故选C．
点评 本题考查函数的图象，考查排除法的运用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
4．i为虚数单位，复数$z=\frac{i-1}{i+1}$的虚部为（ ）
| A． | 1 | B． | 0 | C． | i | D． | 以上都不对 |
5．已知集合A={x|x2-x＞0}，$B=\left\{{x\left|{-\sqrt{3}＜x＜\sqrt{3}}\right.}\right\}$，则（ ）
| A． | A∩B=∅ | B． | A∪B=R | C． | B⊆A | D． | A⊆B |
2．已知全集U为实数集，集合A={x|x2-2x-3＜0}，B={x|y=ln（1-x）}，则A∩（∁UB）为（ ）
| A． | {x|1≤x＜3} | B． | {x|x＜3} | C． | {x|x≤-1} | D． | {x|-1＜x＜1} |
9．已知复数为纯虚数$z=\frac{a+i}{1+i}$（i虚数单位），则实数a=（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
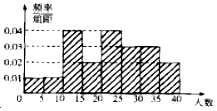为了更好地让学生适应高考网上阅卷，某学校针对该校20个班级进行了“汉字与英语书法大赛”（每个班级只有一个指导老师），并调查了各班参加该比赛的学生人数，根据所得数据，分组成[0，5），[5，10），[10，15），[15，20），[20，25），[25，30），[30，35），[35，40]时，所作的频率分布直方图如图：