题目内容
5.已知集合A={x|x2-x>0},$B=\left\{{x\left|{-\sqrt{3}<x<\sqrt{3}}\right.}\right\}$,则( )| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
分析 先分别求出集合A和B,由此得到A∪B=R.
解答 解:∵集合A={x|x2-x>0}={x|x>1或x<0},
$B=\left\{{x\left|{-\sqrt{3}<x<\sqrt{3}}\right.}\right\}$,
∴A∩B={x|-$\sqrt{3}<x<0$或1<x<$\sqrt{3}$},
A∪B=R.
故选:B.
点评 本题考查并集、交集的求法及应用,是基础题,解题时要认真审题,注意并集、交集定义的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.为了迎接一年一度的元宵节,某商场大楼安装了5个彩灯,它们闪亮的顺序不固定,每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯闪亮的颜色各不相同,记这5个彩灯有序地闪亮一次为一个闪烁,在每个闪烁中,每秒钟有且只有一个彩灯闪亮,且相邻两个闪烁的时间间隔均为5秒,如果要实现所有不同的闪烁,那么需要的时间至少是( )
| A. | 1190秒 | B. | 1195秒 | C. | 1200秒 | D. | 1205秒 |
15.复数z满足z(2-i)=2+i(i为虚数单位),则$\overline z$在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
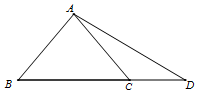 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.


