题目内容
定义在(-∞,+∞)上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,下面是关于f(x)的判断:
①f(x)是周期函数;
②f(x)的图象关于直线x=1对称;
③f(x)在[0,1]上是增函数;④f(2)=f(0).
其中正确的判断是 (把你认为正确的判断都填上)
①f(x)是周期函数;
②f(x)的图象关于直线x=1对称;
③f(x)在[0,1]上是增函数;④f(2)=f(0).
其中正确的判断是
考点:命题的真假判断与应用
专题:简易逻辑
分析:由题意求出函数的周期,判断①,推导④,利用周期对称性,判断②,判断③,即可确定正确结果.
解答:
解:f(x)是定义在R上的偶函数,f(x)关于y轴对称,
则f(-x)=f(x),
又f(x+1)=-f(x)
f(x+2)=f(x+1+1)=-f(x+1)=f(x),
∴2为f(x)的一个周期,命题①正确;
f(x+2)=f(x)=f(-x),
∴f(x)的图象关于直线x=1对称,命题②正确;
∵f(x)在区间[-1,0]上为增函数,f(x)关于y轴对称,所以f(x)在[0,1]上是减函数,命题③错误;
∵2为f(x)的一个周期,∴f(2)=f(0),命题④正确.
故答案为:①②④
则f(-x)=f(x),
又f(x+1)=-f(x)
f(x+2)=f(x+1+1)=-f(x+1)=f(x),
∴2为f(x)的一个周期,命题①正确;
f(x+2)=f(x)=f(-x),
∴f(x)的图象关于直线x=1对称,命题②正确;
∵f(x)在区间[-1,0]上为增函数,f(x)关于y轴对称,所以f(x)在[0,1]上是减函数,命题③错误;
∵2为f(x)的一个周期,∴f(2)=f(0),命题④正确.
故答案为:①②④
点评:本题考查函数的周期性,函数单调性的判断与证明,函数的值,考查分析问题解决问题的能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a,b,c表示三条不同直线,α,β表示两个不同平面,则下列命题中逆命题不成立的是( )
| A、b?β,c是α在β内的射影,若b⊥c,则b⊥a |
| B、b?α,c?α,若c∥α,则b∥c |
| C、c⊥α,若c⊥β,则α∥β |
| D、b?β,若b⊥α,则β⊥α |
如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )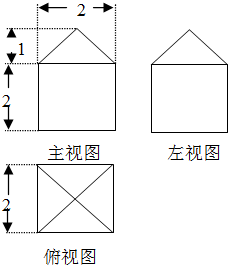

A、(20+4
| ||
| B、21 cm | ||
C、(24+4
| ||
| D、24 cm |
一个几何体的三视图如图所示,则这个几何体的表面积为( )
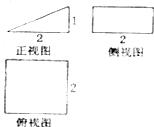

A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
已知x、y的取值如表:从散点图分析,y与x线性相关,且回归方程为
=0.95x+a,则a=( )
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.6 | B、4 |
| C、4.5 | D、条件不足,无法求解 |
 锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.若∠C=50°,则∠IEH的度数=
锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.若∠C=50°,则∠IEH的度数=