题目内容
13.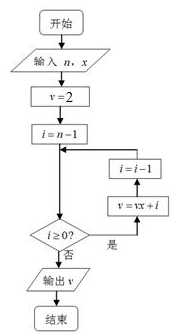 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 66 | B. | 33 | C. | 16 | D. | 8 |
分析 由题意,模拟程序的运行,依次写出每次循环得到的i,v的值,当i=-1时,不满足条件i≥0,跳出循环,输出v的值为66.
解答 解:初始值n=4,x=2,程序运行过程如下表所示:
v=2,
i=4,v=,2×2+3=7,
i=2,v=14+2=16,
i=1,v=16×2+1=33,
i=0,v=33×2+0=66,
i=-1 跳出循环,输出v的值为66,
故选:A.
点评 本题主要考查了循环结构的程序框图的应用,正确依次写出每次循环得到的i,v的值是解题的关键,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.现有1名男同学和2名女同学参加演讲比赛,共有2道演讲备选题目,若每位选手从中有放回地随机选出一道题进行演讲,以下说法不正确的是( )
| A. | 三人都抽到同一题的概率为$\frac{1}{4}$ | |
| B. | 只有两名女同学抽到同一题的概率为$\frac{1}{4}$ | |
| C. | 其中恰有一男一女抽到同一道题的概率为$\frac{1}{2}$ | |
| D. | 至少有两名同学抽到同一题的概率为$\frac{3}{4}$ |
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,过点F作倾斜角为30°的直线与双曲线左右两支各有一个交点,过点F作倾斜角为60°的直线与双曲线右支交于不同的两点,则该双曲线离心率的取值范围是( )
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{2\sqrt{3}}{3}$,2) | C. | [$\frac{2\sqrt{3}}{3}$,2] | D. | (2,+∞) |
1.已知f(x)是定义在R上的奇函数,且周期为2,当x∈(0,1]时,f(x)=1-x,则函数f(x)在[0,2017]上的零点个数是( )
| A. | 1008 | B. | 1009 | C. | 2017 | D. | 2018 |
18.已知集合A={x|x2-2x>0},B=[0,4],则A∩B=( )
| A. | [-4,-1) | B. | (2,4] | C. | [-4,-1)∪(2,4] | D. | [2,4] |
2.已知等差数列{an}中,Sn为其前n项和,S4=π(其中π为圆周率),a4=2a2,现从此数列的前30项中随机选取一个元素,则该元素的余弦值为负数的概率为( )
| A. | $\frac{7}{15}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{30}$ |
3.已知抛物线y2=20x的焦点F恰好为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且点F到双曲线的渐近线的距离是4,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{41}$$-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{21}$$-\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1 |
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.