题目内容
15．已知集合A={x|y=lg（x-1）}，B={x|2${\;}^{{x}^{2}-2x}$＜1}，则A∩B=（ ）| A． | {x|x＞1} | B． | {x|x＞0} | C． | {x|0＜x＜2} | D． | {x|1＜x＜2} |
分析 先分别求出集合A和B，由此利用交集定义能求出A∩B．
解答 解：∵集合A={x|y=lg（x-1）}={x|x＞1}，
B={x|2${\;}^{{x}^{2}-2x}$＜1}={x|0＜x＜2}，
∴A∩B={x|1＜x＜2}．
故选：D．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
3．已知抛物线y2=20x的焦点F恰好为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点，且点F到双曲线的渐近线的距离是4，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{41}$$-\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{21}$$-\frac{{y}^{2}}{4}$=1 | C． | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1 |
10．直线l：y=k（x+$\sqrt{2}$）与曲线C：x2-y2=1（x＜0）相交于P，Q两点，则直线l的倾斜角的取值范围是（ ）
| A． | （$\frac{π}{4}$，$\frac{π}{2}$）∪（$\frac{π}{2}$，$\frac{3π}{4}$） | B． | （$\frac{π}{4}$，$\frac{3π}{4}$） | C． | （0，$\frac{π}{2}$）∪（$\frac{π}{2}$，π） | D． | [0，π） |
20．若α∈（$\frac{π}{2}$，π），则3cos2α=cos（$\frac{π}{4}$+α），则sin2α的值为（ ）
| A． | $\frac{1}{18}$ | B． | -$\frac{1}{18}$ | C． | $\frac{17}{18}$ | D． | -$\frac{17}{18}$ |
7．
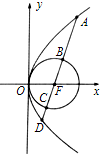如图，抛物线y2=2px（p＞0）和圆x2+y2-px=0，直线l经过抛物线的焦点，依次交抛物线与圆于A，B，C，D四点，|AB|•|CD|=2则p的值为（ ）
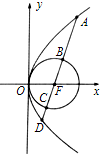如图，抛物线y2=2px（p＞0）和圆x2+y2-px=0，直线l经过抛物线的焦点，依次交抛物线与圆于A，B，C，D四点，|AB|•|CD|=2则p的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |