如图将边长为1的正六边形ABCDEF绕着直线l旋转180°.则旋转所形成的几何体的表面积为2$\sqrt{3}π$ 题目和参考答案——青夏教育精英家教网——

题目内容

14．如图将边长为1的正六边形ABCDEF绕着直线l旋转180°，则旋转所形成的几何体的表面积为2$\sqrt{3}π$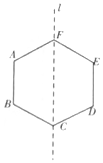

分析由题意，所得几何体的表面积为一个圆柱和两个圆锥的侧面积的和，即可得出结论．

解答解：由题意，所得几何体的表面积为一个圆柱和两个圆锥的侧面积的和，所以S=$2π×\frac{\sqrt{3}}{2}×1$+2×$\frac{1}{2}×2π×\frac{\sqrt{3}}{2}×1$=2$\sqrt{3}π$．
故答案为：2$\sqrt{3}π$．

点评本题考查侧面积的计算，考查学生的计算能力，确定由题意，所得几何体的表面积为一个圆柱和两个圆锥的侧面积的和是关键．

练习册系列答案

百所名校专项期末卷系列答案

伴你学初中生生活系列答案

伴你学英语课堂活动手册系列答案

榜上有名中考新攻略系列答案

北京市各区模拟及真题精选系列答案

备战小升初模拟试题精选系列答案

本土学练系列答案

毕业模拟卷系列答案

变式训练系列答案

博师在线系列答案

相关题目

4．椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（　　）

$\frac{\sqrt{5}}{5}$

$\frac{6\sqrt{5}}{5}$

$\frac{8\sqrt{5}}{5}$

$\frac{4\sqrt{5}}{5}$

已知抛物线x²=2py和$\frac{{x}^{2}}{2}$-y²=1的公切线PQ（P是PQ与抛物线的切点，未必是PQ与双曲线的切点）与抛物线的准线交于Q，F（0，$\frac{P}{2}$），若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|，则抛物线的方程是（　　）

x²=2$\sqrt{3}$y

x²=2$\sqrt{2}$y

2．已知圆C：x²+y²+2x-8y+m=0与抛物线上E：y²=8x的准线l相切，抛物线E上的点P到准线l的距离为d，Q为圆C上任意一点，则|PQ|+d的最小值等于（　　）

9．高三学生小李计划在2017年高考结束后，和其他小伙伴一块儿进行旅游，有3个自然风光景点A，B，C和3个人文历史景点a，b，c可供选择，由于时间和距离原因，只能从中任取4个景点进行参观，其中景点A不能第一个参观，且最后参观的是人文历史景点，则不同的旅游顺序有（　　）

19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两焦点分别为F₁，F₂，短轴的一个端点为点P，△PF₁F₂内切圆的半径为$\frac{b}{3}$．设过点F₂的直线l被椭圆C截得的线段为RS，当l⊥x轴时，|RS|=3
（1）求椭圆C的标准方程；
（2）在x轴上是否存在一点T，使得当l变化时，总有TS与TR所在直线关于x轴对称？若存在，请求出点T的坐标，若不存在，请说明理由．

6．等差数列{a_n}中，a₃+a₄=4，a₅+a₇=6．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）设b_n=a_n•5ⁿ，求{b_n}的前n项和S_n．

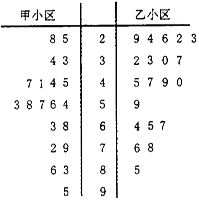某市为了了解全民健身运动开展的效果，选择甲、乙两个相似的小区作对比，一年前在甲小区利用体育彩票基金建设了健身广场，一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本，进行身体综合素质测试，测试得分分数的茎叶图（其中十位为茎，个们为叶）如图：
（1）求甲小区和乙小区的中位数；
（2）身体综合素质测试成绩在60分以上（含60）的人称为“身体综合素质良好”，否则称为“身体综合素质一般”．以样本中的频率作为概率，两小区人口都按1000人计算，填写下列2×2列联表，

	甲小区（有健康广场）	乙小区（无健康广场）	合计
身体综合素质良好	350	300	650
身体综合素质一般	650	700	1350
合计	1000	1000	2000

并判断是否有97.5%把握认为“身体综合素质良好”与“小区是否建设健身广场”有关？

P（K²＞k）	0.10	0.05	0.025	0.01	0.005
k₀	1.706	3.841	5.024	6.635	7.879

（附：k=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$）

4．已知函数f（x）=x³+1，g（x）=2（log₂^x）²-2log₂^x+t-4，若函数F（x）=f（g（x））-1在区间[1，2$\sqrt{2}$]上恰有两个不同的零点，则实数t的取值范围（　　）

[$\frac{5}{2}$，4]

[$\frac{5}{2}$，$\frac{9}{2}$）

[4，$\frac{9}{2}$）

[4，$\frac{9}{2}$]