题目内容
12.曲线f(x)=xlnx在点P(1,0)处的切线l与两坐标轴围成的三角形的面积是$\frac{1}{2}$.分析 求出函数的导数,利用导数的几何意义求出切线的斜率,由点斜式方程可得切线方程,计算切线与坐标轴的交点坐标,即可得出三角形面积.
解答 解:f′(x)=lnx+x•$\frac{1}{x}$=lnx+1,
∴在点P(1,0)处的切线斜率为k=1,
∴在点P(1,0)处的切线l为y-0=x-1,即y=x-1,
∵y=x-1与坐标轴交于(0,-1),(1,0).
∴切线y=x-1与坐标轴围成的三角形面积为S=$\frac{1}{2}$×1×1=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了导数的运用:求切线的方程,考查导数的几何意义,以及三角形的面积计算,属于基础题.

练习册系列答案
相关题目
3.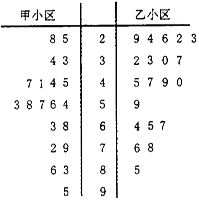 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
(1)求甲小区和乙小区的中位数;
(2)身体综合素质测试成绩在60分以上(含60)的人称为“身体综合素质良好”,否则称为“身体综合素质一般”.以样本中的频率作为概率,两小区人口都按1000人计算,填写下列2×2列联表,
并判断是否有97.5%把握认为“身体综合素质良好”与“小区是否建设健身广场”有关?
(附:k=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
 某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:
某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:(1)求甲小区和乙小区的中位数;
(2)身体综合素质测试成绩在60分以上(含60)的人称为“身体综合素质良好”,否则称为“身体综合素质一般”.以样本中的频率作为概率,两小区人口都按1000人计算,填写下列2×2列联表,
| 甲小区(有健康广场) | 乙小区(无健康广场) | 合计 | |
| 身体综合素质良好 | 350 | 300 | 650 |
| 身体综合素质一般 | 650 | 700 | 1350 |
| 合计 | 1000 | 1000 | 2000 |
| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 1.706 | 3.841 | 5.024 | 6.635 | 7.879 |
20.已知集合A={x|0<x<2},集合B={x|-1<x<1},则A∪B等于( )
| A. | {x|0<x<1} | B. | {x|-1<x<2} | C. | {x|0<x<2} | D. | {x|-1<x<1} |
4.已知函数f(x)=x3+1,g(x)=2(log2x)2-2log2x+t-4,若函数F(x)=f(g(x))-1在区间[1,2$\sqrt{2}$]上恰有两个不同的零点,则实数t的取值范围( )
| A. | [$\frac{5}{2}$,4] | B. | [$\frac{5}{2}$,$\frac{9}{2}$) | C. | [4,$\frac{9}{2}$) | D. | [4,$\frac{9}{2}$] |
1.6名同学合影留念,站成两排三列,则其中甲乙两人不在同一排也不在同一列的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{4}{5}$ |
2.若双曲线$\frac{x^2}{3-m}+\frac{y^2}{m-1}=1$的渐近线方程为$y=±\frac{1}{2}x$,则m的值为( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | $\frac{11}{3}$ | D. | -1或$\frac{1}{3}$ |