题目内容
12.已知△ABC中,D为BC边上一点,∠BAD=∠CAD,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=2,∠BAC=$\frac{π}{3}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=( )| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |
分析 以AD为对角线作平行四边形,在所作平行四边形为菱形,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AD}$、$\overrightarrow{BC}$再计算$\overrightarrow{AD}•\overrightarrow{BC}$.
解答 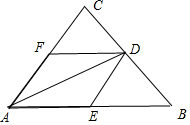 解:以AD为对角线作平行四边形AEDF,其中E在AB上,F在AC上,
解:以AD为对角线作平行四边形AEDF,其中E在AB上,F在AC上,
∵∠BAD=∠CAD,∴平行四边形AEDF是菱形,
设AE=AF=a,则$\overrightarrow{AE}=\frac{a}{3}\overrightarrow{AB}$,$\overrightarrow{AF}=\frac{a}{2}\overrightarrow{AC}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AE}+\overrightarrow{AF}$=$\frac{a}{3}\overrightarrow{AB}+\frac{a}{2}\overrightarrow{AC}$,
∵D在BC上,∴$\frac{a}{3}+\frac{a}{2}=1$,解得a=$\frac{6}{5}$,
∴$\overrightarrow{AD}$=$\frac{2}{5}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}$,又$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,
∴$\overrightarrow{AD}•\overrightarrow{BC}$=($\frac{2}{5}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}$)•($\overrightarrow{AC}-\overrightarrow{AB}$)=$\frac{3}{5}{\overrightarrow{AC}}^{2}$-$\frac{2}{5}{\overrightarrow{AB}}^{2}$-$\frac{1}{5}\overrightarrow{AB}•\overrightarrow{AC}$,
∵${\overrightarrow{AB}}^{2}$=9,${\overrightarrow{AC}}^{2}$=4,$\overrightarrow{AB}•\overrightarrow{AC}$=3×2×cos$\frac{π}{3}$=3,
∴$\overrightarrow{AD}•\overrightarrow{BC}$=$\frac{3}{5}{\overrightarrow{AC}}^{2}$-$\frac{2}{5}{\overrightarrow{AB}}^{2}$-$\frac{1}{5}\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{12}{5}-\frac{18}{5}-\frac{3}{5}$=-$\frac{9}{5}$,
故选C.
点评 本题考查了平面向量的基本定理,数量积运算,属于中档题,作出菱形AEDF是关键,属于中档题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |