题目内容
已知函数f（x）=2cos（ωx+
）（ω＞0，x∈R）的最小正周期为10π．
（1）求函数f（x）的对称轴方程；
（2）设α，β∈[0，
]，f（5α+
）=-
，f（5β-
）=
，求cos（α+β）的值．
| π |
| 6 |
（1）求函数f（x）的对称轴方程；
（2）设α，β∈[0，
| π |
| 2 |
| 5π |
| 3 |
| 6 |
| 5 |
| 5π |
| 6 |
| 16 |
| 17 |
考点：函数y=Asin（ωx+φ）的图象变换,两角和与差的余弦函数
专题：三角函数的图像与性质
分析：（1）由周期求得ω=
，由
x+
=kπ，k∈z，求得对称轴方程．
（2）由 α，β∈[0，
]，f（5α+
）=-
，可得sinα 的值，可得cosα的值．由f（5β-
）=
，求得cosβ的值，可得sinβ 的值，从而求得 cos（α+β）=cosαcosβ-sinαsinβ 的值．
| 1 |
| 5 |
| 1 |
| 5 |
| π |
| 6 |
（2）由 α，β∈[0，
| π |
| 2 |
| 5π |
| 3 |
| 6 |
| 5 |
| 5π |
| 6 |
| 16 |
| 17 |
解答：
解：（1）由条件可知，T=
=10π，∴ω=
，
则由
x+
=kπ⇒x=-
π+5kπ(k∈Z)，
故所求对称轴方程为 x=-
+5kπ，k∈z．
（2）∵α，β∈[0，
]，f（5α+
）=2cos（α+
+
）=-2sinα=-
，可得sinα=
，∴cosα=
．
∵f（5β-
）=2cosβ=
，∴cosβ=
，∴sinβ=
，
∴cos（α+β）=cosαcosβ-sinαsinβ=
×
-
×
=-
．
| 2π |
| ω |
| 1 |
| 5 |
则由
| 1 |
| 5 |
| π |
| 6 |
| 5 |
| 6 |
故所求对称轴方程为 x=-
| 5π |
| 6 |
（2）∵α，β∈[0，
| π |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 6 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
∵f（5β-
| 5π |
| 6 |
| 16 |
| 17 |
| 8 |
| 17 |
| 15 |
| 17 |
∴cos（α+β）=cosαcosβ-sinαsinβ=
| 4 |
| 5 |
| 8 |
| 17 |
| 3 |
| 5 |
| 15 |
| 17 |
| 13 |
| 85 |
点评：本题主要考查函数y=Asin（ωx+φ）的图象特征，余弦函数的对称性、周期性、两角和差的余弦公式、同角三角函数的基本关系、诱导公式的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
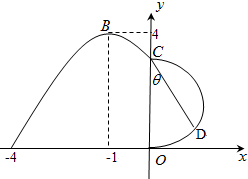如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧．