Question

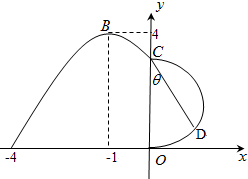如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧．
（1）试确定A，ω和φ的值；
（2）现要在右侧的半圆中修建一条步行道CDO（单位：米），在点C与半圆弧上的一点D之间设计为直线段（造价为2万元/米），从D到点O之间设计为沿半圆弧的弧形（造价为1万元/米）．设∠DCO=θ（弧度），试用θ来表示修建步行道的造价预算，并求造价预算的最大值？（注：只考虑步行道的长度，不考虑步行道的宽度）

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值．
（2）由题意可得CO=2

3

，取CO中点F，求得圆弧段

DO

造价预算为2

3

θ万元，直线段CD造价预算为4

3

cosθ万元，可得步行道造价预算g(θ)=4

3

cosθ+2

3

θ，θ∈(0，

π

2

)． 再利用导数求出函数g（θ）的单调性，从而求得g（θ）的最大值．

解答： 解：（1）因为最高点B（-1，4），所以A=4；

T

4

=-1-(-4)=3⇒T=12，
因为T=

2π

ω

=12⇒ω=

π

6

．
代入点B（-1，4），可得4=4sin[

π

6

×(-1)+φ]⇒sin(φ-

π

6

)=1，
又0＜φ＜π⇒φ=

2π

3

．
（2）由（1）可知：y=4sin(

π

6

x+

2π

3

)

，&x∈[-4，0]

，得点C(0，2

3

)即CO=2

3

，
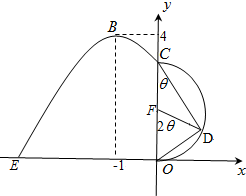
取CO中点F，连结DF，因为弧CD为半圆弧，所以∠DFO=2θ，∠CDO=90°，
即

DO

=2θ×

3

=2

3

θ，则圆弧段

DO

造价预算为2

3

θ万元．
Rt△CDO中，CD=2

3

cosθ，则直线段CD造价预算为4

3

cosθ万元，
所以步行道造价预算g(θ)=4

3

cosθ+2

3

θ，θ∈(0，

π

2

)． 
由g′(x)=4

3

(-sinθ)+2

3

=2

3

(1-2sinθ)得，当θ=

π

6

时，g′（θ）=0，
当θ∈(0，

π

6

)时，g′（x）＞0，即g（θ）在(0，

π

6

)上单调递增；
当θ∈(

π

6

，

π

2

)时，g′（x）＜0，即g（θ）在(

π

6

，

π

2

)上单调递减
所以g（θ）在θ=

π

6

时取极大值，也即造价预算最大值为（6+

3

3

π）万元．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，利用导数研究函数的单调性，根据单调性求函数的最值，属于中档题．