题目内容
已知△ABC中,内角A,B,C的对边分别是a,b,c,面积为S.
(1)求证:a2+b2+c2≥4
S;
(2)求证:tan
tan
,tan
tan
,tan
tan
中至少有一个不小于
.
(1)求证:a2+b2+c2≥4
| 3 |
(2)求证:tan
| A |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
| 1 |
| 3 |
考点:反证法与放缩法,两角和与差的正切函数
专题:证明题,反证法
分析:(1)利用分析法进行证明;
(2)用反证法证明数学命题时,应先假设要证的结论的反面成立,即命题的否定.
(2)用反证法证明数学命题时,应先假设要证的结论的反面成立,即命题的否定.
解答:
证明:(1)要证明a2+b2+c2≥4
S,
只需证明a2+b2+a2+b2-2abcosC≥2
absinC,
只需证明a2+b2≥2absin(C+
),
只需证明a2+b2≥2ab,
只需证明(a-b)2≥0,显然成立,
∴a2+b2+c2≥4
S;
(2)假设tan
tan
,tan
tan
,tan
tan
都不小于
,
则tan
tan
+tan
tan
+tan
tan
<1①
∵tan
tan
+tan
tan
+tan
tan
=tan
(tan
+tan
)+tan
tan
=tan
tan(
+
)[1-tan
tan
]+tan
tan
=1
这与①矛盾,
∴tan
tan
,tan
tan
,tan
tan
中至少有一个不小于
.
| 3 |
只需证明a2+b2+a2+b2-2abcosC≥2
| 3 |
只需证明a2+b2≥2absin(C+
| π |
| 6 |
只需证明a2+b2≥2ab,
只需证明(a-b)2≥0,显然成立,
∴a2+b2+c2≥4
| 3 |
(2)假设tan
| A |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
| 1 |
| 3 |
则tan
| A |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
∵tan
| A |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
| B |
| 2 |
| A |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
=tan
| B |
| 2 |
| A |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
| C |
| 2 |
| A |
| 2 |
这与①矛盾,
∴tan
| A |
| 2 |
| B |
| 2 |
| B |
| 2 |
| C |
| 2 |
| C |
| 2 |
| A |
| 2 |
| 1 |
| 3 |
点评:用反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
执行所示的程序框图,如果输入N=5,则输出的数等于( )
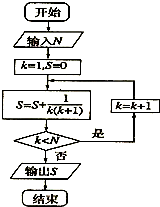

A、
| ||
B、
| ||
C、
| ||
D、
|
 已知抛物线x2=4y,直线l:y=x-2,F是抛物线的焦点.
已知抛物线x2=4y,直线l:y=x-2,F是抛物线的焦点.