题目内容
设实数a,b∈R,函数f(x)=acos
(
sin
+cos
)+b.
(1)若a>0,求f(x)的单调增区间;
(2)若f(x)的最大值为2,最小值为-4,试确定a,b的值.
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
(1)若a>0,求f(x)的单调增区间;
(2)若f(x)的最大值为2,最小值为-4,试确定a,b的值.
考点:三角函数中的恒等变换应用,三角函数的最值
专题:常规题型,三角函数的图像与性质
分析:(1)逆用倍角公式及两角和的正弦公式化成正弦型函数的标准形式,根据正弦函数的单调增区间求函数f(x)的单调区间;
(2)由函数的最大值为2,最小值为-4,构造关于a,b的方程组求解,但要根据a的正负进行分类讨论.
(2)由函数的最大值为2,最小值为-4,构造关于a,b的方程组求解,但要根据a的正负进行分类讨论.
解答:
解:(1)f(x)=acos
(
sin
+cos
)+b
=
acos
sin
+acos2
+b
=
asinx+
+
cosx+b
=asin(x+
)+b+
由-
+2kπ≤x+
≤
+2kπ(k∈Z)
得-
π+2kπ≤x≤
+2kπ(k∈Z)
∴当a>0时,f(x)的单调增区间为[-
+2kπ,
+2kπ](k∈Z);
(2)∵f(x)的最大值为2,最小值为-4,
∴当a>时,a+b+
=2,-a+b+
=-4
解得:a=3,b=-
.
当a<0时,a+b+
=-4,-a+b+
=2
解得:a=-3,b=-
.
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
=
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=asin(x+
| π |
| 6 |
| 1 |
| 2 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
得-
| 2 |
| 3 |
| π |
| 3 |
∴当a>0时,f(x)的单调增区间为[-
| 2π |
| 3 |
| π |
| 3 |
(2)∵f(x)的最大值为2,最小值为-4,
∴当a>时,a+b+
| 1 |
| 2 |
| 1 |
| 2 |
解得:a=3,b=-
| 3 |
| 2 |
当a<0时,a+b+
| 1 |
| 2 |
| 1 |
| 2 |
解得:a=-3,b=-
| 3 |
| 2 |
点评:本题考查了倍角公式及两角和差公式的逆用以及三角函数的图象与性质,解决题目的关键是利用公式化成正弦型函数的标准形式;第(2)问要注意根据a正负进行分类讨论.

练习册系列答案
相关题目
已知命题p:?x∈R,ax>0(a>0且a≠1),则( )
| A、¬p:?x∈R,ax≤0 |
| B、¬p:?x∈R,ax>0 |
| C、¬p:?x0∈R,a x0>0 |
| D、¬p:?x0∈R,a x0≤0 |
f(x)是定义在R上的偶函数,已知函数f(x)在(-∞,0]上单调递减,且f(2)=0,则使f(x)<0的x的取值范围是( )
| A、(-2,0]∪[2,+∞) |
| B、(-2,2) |
| C、(-2,0) |
| D、(2,+∞) |
已知向量
,
满足:|
|=2,|
|=1,且
•
=2,则|
+
|为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | B、4 | C、9 | D、8 |
执行所示的程序框图,如果输入N=5,则输出的数等于( )
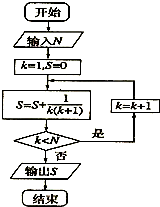

A、
| ||
B、
| ||
C、
| ||
D、
|

 平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.