题目内容
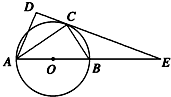 如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.若EB=6,EC=6
如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.若EB=6,EC=6| 2 |
考点:与圆有关的比例线段
专题:直线与圆
分析:连接OC,由弦切角定理推导出OC∥AD.由AD⊥DC,得到DC⊥OC,由切割线定理得到EC2=EB•EA.再由已条件推导出△ECB∽△EAC,由此能求出BC长.
解答:
解:∵AB是⊙O的直径,∠ACB=90°,
∴点C在⊙O上.
连接OC,由弦切角定理得∠OCA=∠OAC=∠DAC,
∴OC∥AD.又∵AD⊥DC,∴DC⊥OC.
∵OC为⊙O半径,∴DC是⊙O的切线.
∵DC是⊙O的切线,∴EC2=EB•EA.
又∵EB=6,EC=6
,∴EA=12,AB=6.
又∵∠ECB=∠EAC,∠CEB=∠AEC,
∴△ECB∽△EAC,∴
=
=
,
∴AC=
BC.
又∵AC2+BC2=AB2=36,∴BC=2
.
故答案为:2
.

∴点C在⊙O上.
连接OC,由弦切角定理得∠OCA=∠OAC=∠DAC,
∴OC∥AD.又∵AD⊥DC,∴DC⊥OC.
∵OC为⊙O半径,∴DC是⊙O的切线.
∵DC是⊙O的切线,∴EC2=EB•EA.
又∵EB=6,EC=6
| 2 |
又∵∠ECB=∠EAC,∠CEB=∠AEC,
∴△ECB∽△EAC,∴
| BC |
| AC |
| EC |
| EA |
| ||
| 2 |
∴AC=
| 2 |
又∵AC2+BC2=AB2=36,∴BC=2
| 3 |
故答案为:2
| 3 |
点评:本题考查与圆有关的线段长的求法,是中档题,解题时要注意切割线定理、相似三角形等知识点的合理运用.

练习册系列答案
相关题目
以正△ABC的顶点A、B为焦点的双曲线恰好平分边AC、BC,则双曲线的离心率为( )
A、
| ||
| B、2 | ||
C、
| ||
D、2
|
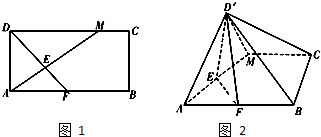 如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.
如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.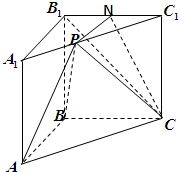 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动