题目内容
14.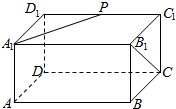 如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.
如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.
分析 先建立空间坐标系,再根据向量的坐标运算和向量的夹角公式计算即可.
解答 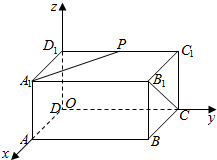 解:以D为坐标原点,以DA为x轴,DC为y轴,DD1为z轴,建立空间坐标系,如图所示,
解:以D为坐标原点,以DA为x轴,DC为y轴,DD1为z轴,建立空间坐标系,如图所示,
∵AD=AA1=1,AB=2,P是C1D1的中点,
∴B1(1,2,1),C=(0,2,0),A1(1,0,1),P(0,1,1),
∴$\overrightarrow{{B}_{1}C}$=(-1,0,-1),$\overrightarrow{{A}_{1}P}$=(-1,1,0),
∴$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1+0+0=1,|$\overrightarrow{{B}_{1}C}$|=$\sqrt{2}$,|$\overrightarrow{{A}_{1}P}$|=$\sqrt{2}$
设$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角为θ,
∴cosθ=$\frac{1}{\sqrt{2}•\sqrt{2}}$=$\frac{1}{2}$,
∴θ=60°,
故答案为:60°,1
点评 本题考查了空间向量的坐标运算以及线线角的求法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若直线x-y-m=0被圆x2+y2-8x+12=0所截得的弦长为$2\sqrt{2}$,则实数m的值为( )
| A. | 2或6 | B. | 0或8 | C. | 2或0 | D. | 6或8 |
19.函数f(x)的图象如图所示,则下列结论正确的是( )
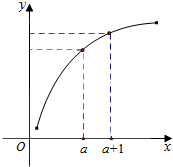

| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
3.若角α的顶点为坐标原点,始边与x轴的非负半轴重合,且终边上一点的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则tanα的值为( )
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |