题目内容
5.若直线x-y-m=0被圆x2+y2-8x+12=0所截得的弦长为$2\sqrt{2}$,则实数m的值为( )| A. | 2或6 | B. | 0或8 | C. | 2或0 | D. | 6或8 |
分析 由已知得圆心(4,0)到直线x-y-m=0的距离d=$\frac{|4-m|}{\sqrt{2}}$=$\sqrt{4-2}$,即可求出实数m的值.
解答 解:x2+y2-8x+12=0,可化为(x-4)2+y2=4
∵直线x-y-m=0被圆x2+y2-8x+12=0所截得的弦长为$2\sqrt{2}$,
∴圆心(4,0)到直线x-y-m=0的距离d=$\frac{|4-m|}{\sqrt{2}}$=$\sqrt{4-2}$=$\sqrt{2}$,
∴解得m=2或6,
故选:A.
点评 本题考查实数值的求法,是基础题,解题时要注意圆的性质和点到直线的距离公式的合理运用.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
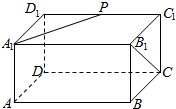 如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.
如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.