题目内容
设全集为R,集合A={x|-1≤x<3},B={x|2x-4≥x-2},
1)求:A∪B,∁R(A∩B);
2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
1)求:A∪B,∁R(A∩B);
2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
考点:子集与交集、并集运算的转换
专题:计算题,集合
分析:(1)由A与B,求出两集合的交集,并集,以及交集的补集即可;
(2)B∪C=C,则B⊆C,即可求实数a的取值范围.
(2)B∪C=C,则B⊆C,即可求实数a的取值范围.
解答:
解:(1)∵A={x|-1≤x<3},B={x|x≥2},全集为R,
∴A∪B={x|x≥-1},A∩B={x|2≤x<3},CR(A∩B)={x|x<2或x≥3};
(2)C={x|2x+a>0}={x|x>-
},
∵B∪C=C,
∴B⊆C,
∴-
<2,
∴a>-4.
∴A∪B={x|x≥-1},A∩B={x|2≤x<3},CR(A∩B)={x|x<2或x≥3};
(2)C={x|2x+a>0}={x|x>-
| a |
| 2 |
∵B∪C=C,
∴B⊆C,
∴-
| a |
| 2 |
∴a>-4.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
下列命题中正确的是( )
A、“m=
| ||
| B、“直线l垂直平面α内无数条直线”是“直线l垂直于平面α”的充分条件 | ||
| C、已知a,b,c为非零向量,则“a•b=a•c”是“b=c”的充要条件 | ||
| D、p:存在x∈R,x2+2x+2≤0,则¬p:任意x∈R,x2+2x+2>0. |
分式方程
+1=
的解是( )
| x-3 |
| x-2 |
| 3 |
| 2-x |
| A、2 | B、1 | C、-1 | D、-2 |
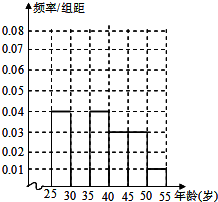 某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”.通过调查分别得到如图所示统计表,如图2所示各年龄段人数频率分布直方图.
某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”.通过调查分别得到如图所示统计表,如图2所示各年龄段人数频率分布直方图.