题目内容
17.若f(x)是定义在R上的函数,对任意的实数x,都有f(x+3)≥f(x)+3和f(x+2)≤f(x)+2,且f(1)=1,则f(2 017)的值为2017.分析 根据题意,分析可得f(x+6)=f(x)+6,进而分析可得f(2017)=f(336×6+1)=f(1)+336×6,计算可得答案.
解答 解:根据题意,由f(x+3)≥f(x)+3得f(x+6)≥f(x+3)+3≥f(x)+6,
由f(x+2)≤f(x)+2得f(x+6)≤f(x+4)+2≤f(x+2)+4≤f(x)+6,
所以f(x+6)=f(x)+6,
则f(2017)=f(336×6+1)=f(1)+336×6=2017;
故答案为:2017.
点评 本题考查函数的求值,关键是分析f(x+6)=f(x)+6.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.已知f(x)=sinxcosx+$\sqrt{3}$cos2x-$\frac{\sqrt{3}}{2}$,将f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到y=g(x)的图象.若对任意实数x,都有g(a-x)=g(a+x)成立,则$g(a+\frac{π}{4})$=( )
| A. | $1+\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | 0 |
5.已知函数f(x)=2cos(ωx+φ)(ω>0)是奇函数,其图象与直线y=-2的交点间的最小距离是π,则( )
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=2,φ=π | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | D. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ |
6.已知正方形ABCD的边长为6,M在边BC上且BC=3BM,N为DC的中点,则$\overrightarrow{AM}•\overrightarrow{BN}$=( )
| A. | -6 | B. | 12 | C. | 6 | D. | -12 |
7.若函数$f(x)=sin2ωx+2\sqrt{3}{cos^2}ωx-\sqrt{3}(ω>0)$在$[\frac{π}{2},π]$上单调递减,则ω的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{4}]$ | B. | $[\frac{1}{6},\frac{7}{12}]$ | C. | $[\frac{1}{4},\frac{1}{2}]$ | D. | $[0,\frac{1}{2}]$ |
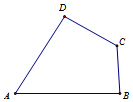 如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.
如图,A,B,C,D为平面四边形ABCD的四个内角,若A+C=180°,AB=6,BC=4,CD=5,AD=5,则四边形ABCD面积是10$\sqrt{6}$.