题目内容
17.直线y=2b与双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左支、右支分别交于B,C两点,A为右顶点,O为坐标原点,若∠AOC=∠BOC,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{\sqrt{15}}}{2}$ | D. | $\frac{{\sqrt{19}}}{2}$ |
分析 利用条件得出∠AOC=60°,C($\frac{2\sqrt{3}}{3}$b,2b),代入双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1,可得$\frac{\frac{4}{3}{b}^{2}}{{a}^{2}}$-4=1,b=$\frac{\sqrt{15}}{2}$a,即可得出结论.
解答 解:∵∠AOC=∠BOC,
∴∠AOC=60°,
∴C($\frac{2\sqrt{3}}{3}$b,2b),
代入双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1,可得$\frac{\frac{4}{3}{b}^{2}}{{a}^{2}}$-4=1,∴b=$\frac{\sqrt{15}}{2}$a,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{19}}{2}$a,
∴e=$\frac{c}{a}$=$\frac{\sqrt{19}}{2}$,
故选D.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
9.执行如图所示的程序框图,则输出的k的值是( )
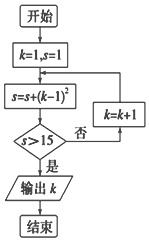

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.若函数f(x)是奇函数,且在(0,+∞)上是增函数,又f(-3)=0,则(x-2)f(x)<0的解集是( )
| A. | (-3,0)∪(2,3) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(2,+∞) |
6.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
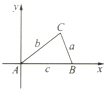 补全用解析法证明余弦定理的过程.
补全用解析法证明余弦定理的过程.