题目内容
sinα=3cosα，则tanα= ．
考点：同角三角函数间的基本关系
专题：三角函数的求值
分析：已知等式两边除以cosα，利用同角三角函数间基本关系化简求出tanα的值即可．
解答：
解：∵sinα=3cosα，
∴
=3，
则tanα=3，
故答案为：3
∴
| sinα |
| cosα |
则tanα=3，
故答案为：3
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
相关题目
已知α是△ABC的一个内角，tanα=
，则cos（α+
）等于（ ）
| 3 |
| 4 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设x＞0，则“a≥1”是“x+
≥2恒成立”的（ ）
| a |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知直线l1：ax+y+2=0和直线l2：x+ay+2=0平行，则实数a的值为（ ）
| A、1 | ||
| B、-1 | ||
| C、-1和1 | ||
D、
|
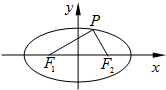已知点P（m，4）是椭圆