题目内容
已知数列{an}是公差不为0的等差数列,其前n项和为Sn,a1,a2,a4成等比数列,2a5=S3+8
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}的前n项和Tn=
,对任意n≥2且n∈N*,不等式bn<kTn恒成立,求实数k的取值范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}的前n项和Tn=
| 3n |
| an+1 |
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)利用数列{an}是公差不为0的等差数列,a1,a2,a4成等比数列,2a5=S3+8,建立方程,求出a1=d=2,即可求数列{an}的通项公式;
(Ⅱ)
=1-
=
-
>
,利用对任意n≥2且n∈N*,不等式bn<kTn恒成立,即可求实数k的取值范围.
(Ⅱ)
| bn |
| Tn |
| Tn |
| Tn-1 |
| 2 |
| 3 |
| 2 |
| 3(2n-1) |
| 2 |
| 3 |
解答:
解:(Ⅰ)∵数列{an}是公差不为0的等差数列,a1,a2,a4成等比数列,2a5=S3+8,
∴(a1+d)2=a1(a1+3d),2(a1+4d)=3a1+3d+8,d≠0,
∴a1=d=2,
∴an=2n;
(Ⅱ)∵数列{bn}的前n项和Tn=
,
∴n=1时,
=1;
n≥2时,bn=Tn-Tn-1,∴
=1-
=
-
>
,
∵对任意n≥2且n∈N*,不等式bn<kTn恒成立,
∴k≥
.
∴(a1+d)2=a1(a1+3d),2(a1+4d)=3a1+3d+8,d≠0,
∴a1=d=2,
∴an=2n;
(Ⅱ)∵数列{bn}的前n项和Tn=
| 3n |
| an+1 |
∴n=1时,
| b1 |
| T1 |
n≥2时,bn=Tn-Tn-1,∴
| bn |
| Tn |
| Tn-1 |
| Tn |
| 2 |
| 3 |
| 2 |
| 3(2n-1) |
| 2 |
| 3 |
∵对任意n≥2且n∈N*,不等式bn<kTn恒成立,
∴k≥
| 2 |
| 3 |
点评:本题考查等差数列与等比数列的综合,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
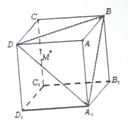 如图,在棱长为1的正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m,n,p分别是点M到平面ADD1A1,平面ABB1A1,平面ABCD的距离,若f(M)=(
如图,在棱长为1的正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m,n,p分别是点M到平面ADD1A1,平面ABB1A1,平面ABCD的距离,若f(M)=(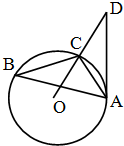 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为