题目内容
写出角的终边在图中阴影区域内角的集合(包括边界)


考点:终边相同的角
专题:三角函数的求值
分析:由题意直接利用终边相同的角的集合的表示方法表示即可.
解答:
解:(1)图中阴影区域内的角的集合:{θ|k•360°+45°≤θ≤k•360°+90°}∪{θ|k•360°+180°≤θ≤k•360°+225°}.k∈Z.
(2)图中阴影区域内的角的集合:{θ|k•90°≤θ≤k•90°+45°}.k∈Z.
(3)图中阴影区域内的角的集合:{θ|k•360°-120°≤θ≤k•360°+150°}.k∈Z.
(2)图中阴影区域内的角的集合:{θ|k•90°≤θ≤k•90°+45°}.k∈Z.
(3)图中阴影区域内的角的集合:{θ|k•360°-120°≤θ≤k•360°+150°}.k∈Z.
点评:本题考查角的表示方法,象限角的表示方法,基本知识的考查.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
F(-c,0)是双曲线
-
=1(a>0,b>0)的左焦点,P是抛物线y2=4cx上一点,直线FP与圆x2+y2=a2相切于点E,且PE=FE,若双曲线的焦距为2
+2,则双曲线的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、
| ||||
B、
| ||||
| C、4 | ||||
| D、2 |
已知向量
=(2x,1),向量
=(-4,2),若
∥
,则
+
为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-2,2) |
| B、(-6,3) |
| C、(2,-1) |
| D、(6,-3) |
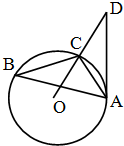 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为