题目内容
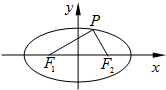 已知点P(m,4)是椭圆
已知点P(m,4)是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设|PF1|=m,|PF2|=n,|F1F2|=2c,由椭圆的定义可得m+n=2a,再由三角形的面积公式以及内切圆的圆心与三个顶点将三角形△PF1F2分成三个小三角形,分别求面积再求和,得到a,c的方程,由离心率公式计算即可得到.
解答:
解:设|PF1|=m,|PF2|=n,|F1F2|=2c,
由椭圆的定义可得m+n=2a,
由三角形的面积公式可得
S△PF1F2=
×2c×4=4c,
由△PF1F2的内切圆的半径为
,
则S△PF1F2=
×
(m+n+2c)=
(2a+2c)=
(a+c),
即有4c=
(a+c),
即为5c=3a,
则离心率e=
=
.
故答案为:
.
由椭圆的定义可得m+n=2a,
由三角形的面积公式可得
S△PF1F2=
| 1 |
| 2 |
由△PF1F2的内切圆的半径为
| 3 |
| 2 |
则S△PF1F2=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
即有4c=
| 3 |
| 2 |
即为5c=3a,
则离心率e=
| c |
| a |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查椭圆的定义和性质,考查三角形的面积公式和面积的分割法,考查离心率的求法,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
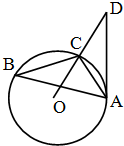 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为