题目内容
化简:2
+
= .
| 1+sin8 |
| 2+2cos8 |
考点:三角函数中的恒等变换应用
专题:
分析:先由1+sin8=sin24+cos24+2sin4cos4=(sin4+cos4)2,2+2cos8=2(1+cos8)=2(1+2cos24-1)=4cos24对原式进行去根号,再根据角的范围确定符号.
解答:
解:∵2
+
=2
+
=2|sin4+cos4|+2|cos4|
又∵4∈(π,
)
∴原式=-2sin4-4cos4
故答案为:-2sin4-4cos4
| 1+sin8 |
| 2+2cos8 |
| sin24+cos24+2sin4cos4 |
| 2(1+ cos8) |
=2|sin4+cos4|+2|cos4|
又∵4∈(π,
| 3π |
| 2 |
∴原式=-2sin4-4cos4
故答案为:-2sin4-4cos4
点评:本题主要考查三角基本关系式和二倍角公式.这里要注意角的范围给三角函数带来的符号问题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知点P(x,y)在以原点为圆心的单位圆上运动,则点Q(x+y,xy)的轨迹是( )
| A、圆 | B、抛物线 | C、椭圆 | D、双曲线 |
(本小题满分12分)每年春季在北京举行的“中国国际马拉松赛”活动,已经成为最具影响力的全民健身活动之一,每年的参与人数不断增多.然而也有部分人对该活动的实际效果提出了质疑,对此,某新闻媒体进行了网上调查,在所有参与调查的人中,持“支持”、“保留意见”和“不支持”态度的人数如下表所示:
支持 | 保留意见 | 不支持 | |
男 | 800 | 450 | 200 |
女 | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取 个人,已知从持“支持”态度的人中抽取了
个人,已知从持“支持”态度的人中抽取了 人,求
人,求 的值;
的值;
(2)接受调查的人同时要对这项活动进行打分,其中 人打出的分数如下:
人打出的分数如下:
 ,
, ,
, ,
, ,
, ,
, ,把这
,把这 个人打出的分数看作一个总体,从中任取
个人打出的分数看作一个总体,从中任取 个数,
个数,
求这两个数与总体平均数之差的绝对值都不超过 的概率.
的概率.
 在港口
在港口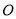 正东方
正东方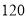 海里处,小岛
海里处,小岛 在港口
在港口 北偏东
北偏东 方向和港口
方向和港口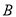 北偏西
北偏西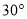 方向上,一艘科学考察船从港口O出发,沿北偏东
方向上,一艘科学考察船从港口O出发,沿北偏东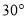 的
的 方向以每小时
方向以每小时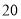 海里的速度驶离港口
海里的速度驶离港口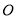 ,一艘快艇从港口B出发,以每小时
,一艘快艇从港口B出发,以每小时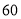 海里的速度驶向小岛
海里的速度驶向小岛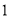 小时,问快艇驶离港口
小时,问快艇驶离港口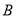 后最少要经过多少时间才能和考察船相遇?
后最少要经过多少时间才能和考察船相遇?
 中,若
中,若 ,则
,则 的最小值是 .
的最小值是 . 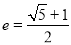 的双曲线
的双曲线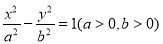 为黄金双曲线.如图是双曲线
为黄金双曲线.如图是双曲线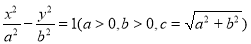 的图象,给出以下几个说法:
的图象,给出以下几个说法: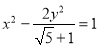 是黄金双曲线;
是黄金双曲线;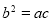 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;