题目内容
2.如图为某几何体的三视图,则该几体的体积为( )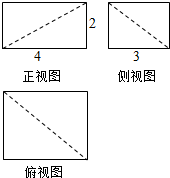
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
分析 由已知中的三视图可得:该几何体是一个长方体切去右后下角的三棱锥所得的组合体,分别求出各部分体积,相减可得答案.
解答 解:由已知中的三视图可得:该几何体是一个长方体切去右后下角的三棱锥所得的组合体,
长方体的体积为:2×3×4=24,
切去的三棱锥的体积为:$\frac{1}{3}$×($\frac{1}{2}$×3×4)×2=4,
故组合体的体积V=20,
故选:C
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 对于函数f:A→B,其值域是集合B | |
| B. | 函数y=1与y=x0是同一个函数 | |
| C. | 两个函数的定义域、对应关系相同,则表示同一个函数 | |
| D. | 映射是特殊的函数 |
17.根据如图所示的框图,当输入的x=3时,则输出的y为( )


| A. | 19 | B. | 10 | C. | 9 | D. | 0 |
7.在空间四边形OABC中,G是△ABC的重心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OG}$=( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | 3$\overrightarrow{a}$+3$\overrightarrow{b}$+3$\overrightarrow{c}$ |
14.设i为虚数单位,复数z=i(5-i)在平面内对应的点的坐标为( )
| A. | (1,5) | B. | (l,-5) | C. | (-1,5) | D. | (-1,-5) |
11.从一个正方体中截去部分几何体,得到的剩余几何体的三视图如图,则此几何体的体积是( )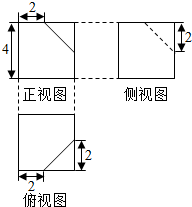

| A. | 64 | B. | $\frac{122}{3}$ | C. | $\frac{188}{3}$ | D. | $\frac{47}{6}$ |
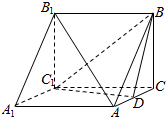 在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.