题目内容
3.某几何体的三视图如图所示,则该几何体的表面积为60.
分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥所得的组合体,分别求出各个面的面积,相加可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥所得的组合体,
其直观图如下图所示:
底面ABC是两直角边分别为3和4的直角三角形,面积为:$\frac{1}{2}$×3×4=6,
侧面ABED是直角梯形,面积为:$\frac{1}{2}$×(2+5)×4=14,
侧面ACFD是矩形,面积为:3×5=15,
侧面BCFE是直角梯形,面积为:$\frac{1}{2}$×(2+5)×$\sqrt{{3}^{2}+{4}^{2}}$=$\frac{35}{2}$,
上底面DEF是直角边分别为:3和$\sqrt{{3}^{2}+{4}^{2}}$的直角三角形,面积为:$\frac{1}{2}$×3×$\sqrt{{3}^{2}+{4}^{2}}$=$\frac{15}{2}$,
故几何体的表面积S=6+14+15+$\frac{35}{2}$+$\frac{15}{2}$=60,
故答案为:60
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 对于函数f:A→B,其值域是集合B | |
| B. | 函数y=1与y=x0是同一个函数 | |
| C. | 两个函数的定义域、对应关系相同,则表示同一个函数 | |
| D. | 映射是特殊的函数 |
14.设i为虚数单位,复数z=i(5-i)在平面内对应的点的坐标为( )
| A. | (1,5) | B. | (l,-5) | C. | (-1,5) | D. | (-1,-5) |
11.从一个正方体中截去部分几何体,得到的剩余几何体的三视图如图,则此几何体的体积是( )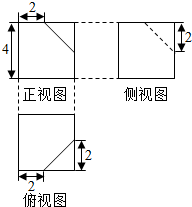

| A. | 64 | B. | $\frac{122}{3}$ | C. | $\frac{188}{3}$ | D. | $\frac{47}{6}$ |