题目内容
19.已知S为数列{an}的前n项和,若an(4+cosnπ)=n(2-cosnπ),則S20=122.分析 分n为奇数、偶数求出各自的通项公式,进而利用等差数列的求和公式计算即得结论.
解答 解:当n=2k+1时,cosnπ=-1,
∴3an=3n,即an=n;
当n=2k+2时,cosnπ=1,
∴5an=n,即an=$\frac{1}{5}$n;
∴S2n=(1+3+5+…+2n-1)+$\frac{1}{5}$(2+4+6+…+2n)
=$\frac{n(1+2n-1)}{2}$+$\frac{1}{5}$•$\frac{n(2+2n)}{2}$
=$\frac{n(6n+1)}{5}$,
∴S20=$\frac{10(6×10+1)}{5}$=122,
故答案为:122.
点评 本题考查数列的求和,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.“α是第一象限角”是“关于x,y的方程x2sinα+y2cosα=1所表示的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.在空间四边形OABC中,G是△ABC的重心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OG}$=( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | 3$\overrightarrow{a}$+3$\overrightarrow{b}$+3$\overrightarrow{c}$ |
14.设i为虚数单位,复数z=i(5-i)在平面内对应的点的坐标为( )
| A. | (1,5) | B. | (l,-5) | C. | (-1,5) | D. | (-1,-5) |
11.从一个正方体中截去部分几何体,得到的剩余几何体的三视图如图,则此几何体的体积是( )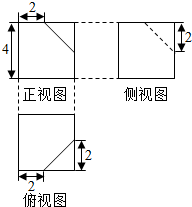

| A. | 64 | B. | $\frac{122}{3}$ | C. | $\frac{188}{3}$ | D. | $\frac{47}{6}$ |