抛物线y=3x2的焦点坐标是,准线方程是y=-$\frac{1}{12}$．题目和参考答案——青夏教育精英家教网——

题目内容

10．抛物线y=3x²的焦点坐标是（0，$\frac{1}{12}$）；准线方程是y=-$\frac{1}{12}$．

分析求出抛物线的标准方程，然后求解焦点坐标以及准线方程．

解答解：抛物线y=3x²的标准方程为：x²=$\frac{1}{3}$y，可得p=$\frac{1}{6}$，抛物线的焦点坐标（0，$\frac{1}{12}$），准线方程y=-$\frac{1}{12}$．
故答案为：（0，$\frac{1}{12}$），y=-$\frac{1}{12}$．

点评本题考查抛物线的简单性质的应用，基本知识的考查．

练习册系列答案

一天一练系列答案

一线调研今年新试卷系列答案

金版课堂课时训练系列答案

单元全能练考卷系列答案

小学同步全程测试卷一考通系列答案

新黄冈兵法密卷系列答案

特优练考卷系列答案

一通百通顶尖单元练系列答案

快乐AB卷系列答案

轻松赢考期末卷系列答案

相关题目

20．若（2x+$\sqrt{3}$）³=a₀+a₁x+a₂x²+a₃x³，则（a₀+a₂）²-（a₁+a₃）²的值为（　　）

1．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），k为何值时下列各式成立？
（1）（k$\overrightarrow{a}$+$\overrightarrow{b}$）⊥（$\overrightarrow{a}$-3$\overrightarrow{b}$）；
（2）（k$\overrightarrow{a}$+$\overrightarrow{b}$）∥（$\overrightarrow{a}$-3$\overrightarrow{b}$）

18．已知函数f（x）=sinx+cosx-sinxcosx
（1）若x∈[0，π]，sinx，cosx是方程x²-2ax-3a=0（a≠0）的两实根，求sinx-cosx的值；
（2）求函数f（x）在区间[$\frac{π}{2}$，π]上的最大值．

5．设A，B，C，D是空间四个不共面的点，以$\frac{1}{2}$的概率在每对点之间一条边，任意两对点之间是否连边是相互独立的，则A，B可用（一条边或若干条边组成的）空间折线连接的概率为$\frac{3}{4}$．

15．从5位男生，4位女生中选出5名代表，则
（1）男生甲当选且女生A不能当选，有几种选法？
（2）至少有一个女生当选，有几种选法？
（3）最多有2个女生当选，有几种选法？
（4）若选出5名代表为3男2女，并进行大会发言，有多少种不同的发言顺序？

2．下列表格中，不是某个随机变量的分布列的是（　　）

X	-2	0	2	4
P	0.5	0.2	0.3	0

X	0	1	2
P	0.7	0.15	0.15

X	1	2	3
P	$-\frac{1}{3}$	$\frac{1}{2}$	$\frac{2}{3}$

X	1	2	3
P	lg1	lg2	lg5

19．把-$\frac{11}{4}$π表示成2kπ+θ（k∈Z）的形式，且使θ∈（0，2π），则θ的值为（　　）

$\frac{5}{4}π$

$\frac{3}{4}π$

$\frac{1}{4}π$

$\frac{7}{4}π$

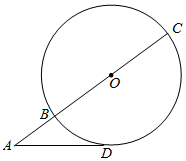如图，BC为⊙O的直径，且BC=6，延长CB与⊙O在点D处的切线交于点A，若AD=4，则AB=2．