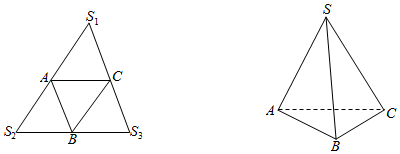题目内容
5.设A,B,C,D是空间四个不共面的点,以$\frac{1}{2}$的概率在每对点之间一条边,任意两对点之间是否连边是相互独立的,则A,B可用(一条边或若干条边组成的)空间折线连接的概率为$\frac{3}{4}$.分析 每对点之间是否连边有2种可能,共有26=64种情况,再分有AB边,无AB边但有CD边和无AB边也无CD边三种情况下A,B可用折线连接数总和,由此能求出A,B可用折线连接的概率.
解答 解:每对点之间是否连边有2种可能,共有26=64种情况,
考虑其中A,B可用折线连接的情况数.
(1)有AB边:共25=32种情况;
(2)无AB边,但有CD边:此时A,B可用折线相连,当且仅当A与C、D中至少一点相连,且B与C、D中至少一点相连,
这样的情况数为(22-1)(22-1)=9;
(3)无AB边,也无CD边:此时AC、BD相连有22=4种,
AD,DB相连也有22种情况,
但其中AC,CB,AD,DB均相连的情况被重复计了一次,
故A、B可用折线连结的情况数为22+22-1=7,
以上三种情况数总和为:32+9+7=48,
故A,B可用折线连接的概率为:p=$\frac{48}{64}=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
17.已知f(x)=sinx+cosx+sin2x,若?t∈R,x∈R,asint+2a+1≥f(x)恒成立,则实数a的取值范围是( )
| A. | (-∞,$\sqrt{2}$] | B. | [$\sqrt{2}$-1,+∞) | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
14.若某项试验的成功率是失败率的2倍,用离散型随机变量X描述1次试验成功的次数,则P(X=1)等于( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
11.如果P1,P2,…,Pn是抛物线C:y2=4x上的点,它们的横坐标依次为x1,x2,…,xn,F是抛物线C的焦点,若x1+x2+…+xn=10,则|P1F|+|P2F|+…+|PnF|=( )
| A. | n+10 | B. | n+20 | C. | 2n+10 | D. | 2n+20 |