题目内容
已知f（x）=asinx+
+2，若f（ln2）=4，则f（ln
）= ．
| 3 | x |
| 1 |
| 2 |
考点：函数的值
专题：函数的性质及应用
分析：利用函数的性质和对数的性质求解．
解答：
解：∵f（x）=asinx+
+2，
∴f（ln2）=asin（ln2）+
+2=4，
∴asin（ln2）+
=2，
∴f（ln
）=-（asin（ln2）+
）+2=-2+2=0．
故答案为：0．
| 3 | x |
∴f（ln2）=asin（ln2）+
| 3 | ln2 |
∴asin（ln2）+
| 3 | ln2 |
∴f（ln
| 1 |
| 2 |
| 3 | ln2 |
故答案为：0．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={x∈R|x2-2x-3＜0}，B={x∈R|-2＜x＜2}，则A∩B=（ ）
| A、（-1，1） |
| B、（-1，2） |
| C、{-1，0} |
| D、{0，1} |
设A={x|x2+x-6=0}，B={x|ax+1=0}，满足A?B，则a取值的集合是（ ）
A、{-
| ||||||
B、{-
| ||||||
C、{
| ||||||
D、{0，-
|
已知全集A={3，4，5}，B={1，3，6}，则A∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{1，6} |
| D、{2，4，5，7} |
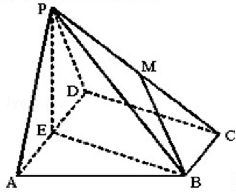如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD中点，M是棱PC的中点，PA=PD=2，BC=