题目内容
设A={x|x2+x-6=0},B={x|ax+1=0},满足A?B,则a取值的集合是( )
A、{-
| ||||||
B、{-
| ||||||
C、{
| ||||||
D、{0,-
|
考点:集合的包含关系判断及应用
专题:集合
分析:由A?B,可分B=∅和B≠∅两种情况进行讨论,根据集合包含关系的判断和应用,分别求出满足条件的a值,并写成集合的形式即可得到答案.
解答:
解:∵A={x|x2+x-6=0}={-3,2}
又∵A?B,当a=0,ax+1=0无解,故B=∅,满足条件
若B≠∅,则B={-3},或Q={2},
即a=
,或a=-
,
故满足条件的实数a∈{0,
,-
};
故选D.
又∵A?B,当a=0,ax+1=0无解,故B=∅,满足条件
若B≠∅,则B={-3},或Q={2},
即a=
| 1 |
| 3 |
| 1 |
| 2 |
故满足条件的实数a∈{0,
| 1 |
| 3 |
| 1 |
| 2 |
故选D.
点评:本题考查了集合的包含关系判断及应用,容易出错的是:①忽略B=∅的情况,②忽略题目要求,答案没用集合形式表示.

练习册系列答案
相关题目
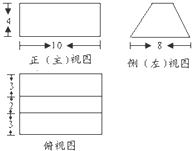
某几何体的三视图如图所示,则该几何体的体积为( )

| A、240 | ||
| B、200 | ||
C、
| ||
D、
|