题目内容
已知关于x的不等式|x+8|+|x-a|≤1的解集不是空集,则a的最小值是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由已知关于x的不等式|x+8|+|x-a|≤1的解集不是空集可得此不等式有解,根据绝对值的几何意义得到|a+8|≤1,解得-1≤a+8≤1,得到a的最小值为-9.
解答:
解:因为关于x的不等式|x+8|+|x-a|≤1的解集不是空集,所以|a+8|≤1,解得-1≤a+8≤1,得到a的最小值为-9.
故答案为:-9.
故答案为:-9.
点评:本题考查了绝对值不等式的解法以及绝对值的几何意义,属于基础题.

练习册系列答案
相关题目
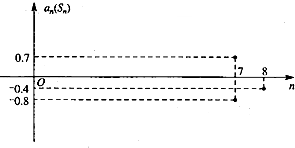 设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )
设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )| A、当n=4时,Sn取得最大值 |
| B、当n=3时,Sn取得最大值 |
| C、当n=4时,Sn取得最小值 |
| D、当n=3时,Sn取得最大值 |
设y1=0.3
,y2=0.4
,y3=0.4
( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| A、y3<y2<y1 |
| B、y1<y2<y3 |
| C、y2<y3<y1 |
| D、y1<y3<y2 |
已知向量
,
的模均为2,且<
,
>=
,若向量
满足|
-(
+
)|=
,则|
|的取值范围为( )
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| c |
| c |
| a |
| b |
| 2 |
| c |
A、[2-
| ||||
B、[0,2+
| ||||
C、[2-
| ||||
| D、[0,4] |
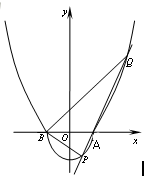 如图,由半椭圆x2+
如图,由半椭圆x2+