题目内容

已知a＞b且ab=2，则
a2+b2-
3
2
ab
a-b
的最小值为
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：本题可以通过配凑法，结合题中条件，将原式化成积为定值的情况，利用基本不等式得出本题结论．
解答： 解：∵a＞b，
∴a-b＞0．
∵ab=2，
∴
a2+b2-
3
2
ab
a-b
=
(a-b)2+
1
2
ab
a-b
=(a-b)+
1
a-b
≥2
(a-b)×
1
a-b
=2．
当且仅当
a=2
b=1
或
a=-1
b=-2
时取等号．
故答案为：2．
点评：本题考查的是基本不等式，注意不等式使用的条件．本题有一定的难度，属于中档题．
练习册系列答案
相关题目
若a＞b，x＞y，则下列不等式中正确的是（　　）
A、a-x＞b-y
B、ax＞by
C、
a
y
＞
b
x
D、x-b＞y-a
若（x-
1
2
）n的展开式中第3项的二项式系数是10，则展开式中所有项系数之和为（　　）
A、
1
64
B、
1
32
C、-
1
64
D、-
1
32
已知函数f（x）=log
1
2
(x2-ax-a)的值域为R，且在（-∞，1-
3
）上是增函数，则a的取值范围是
 
．
已知f（x）=x3+ax2+3x-9在x=-3处取得极值．
（1）求a值；
（2）求函数f（x）的单调递增区间．
已知等差数列{an}中an=21-3n，求当n为多少时，Sn有最大值且求出最大值．
直线
x=3-tcos20°
y=tsin(-20°)
（t为参数）的倾斜角是（　　）
A、20°B、70°
C、110°D、160°
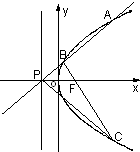已知曲线W上的动点M到点F（1，0）的距离等于它到直线x=-1x=-1的距离．过点P（-1，0）任作一条直线l与曲线W交于不同的两点A、B，点A关于x轴的对称点为C．
（Ⅰ）求曲线W的方程；
（Ⅱ）求△PBC面积S的取值范围．
一个不透明的口袋中装有形状相同的红球、黄球和蓝球，若摸出一球为红球的概率为
1
5
，黄球的概率为
1
4
，袋中红球有4个，则袋中蓝球的个数为（　　）
A、5个B、11个C、4个D、9个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网