题目内容
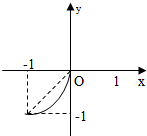 已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )
已知定义在(-1,0)上的函数y=f(x)的图象如图所示,对于满足-1<x1<x2<0的任意x1,x2,错误的结论是( )| A、当x∈(-1,0)时,x>f(x) |
| B、当x∈(-1,0)时,导函数f′(x)为增函数 |
| C、f(x2)-f(x1)≤x2-x1 |
| D、x1f(x2)>x2f(x1) |
考点:函数的图象
专题:函数的性质及应用,导数的概念及应用
分析:抓住函数图象,研究对应函数的性质.
解答:
解:对于A选项,由图象可以看出,x∈(-1,0)时,直线y=x的图象在函数y=f(x)图象的上方,即x>f(x),A选项正确;
对于B选项,导函数f′(x)即为y=f(x)图象上任一点处切线的斜率,递增,即B选项正确;
对于C选项,等价于x1-f(x1)≤x2-f(x2),而函数y=x-f(x)的导函数为y′=1-f′(x),其符号先正后负,即函数y=x-f(x)先增后减,故x1-f(x1)与x2-f(x2)的大小关系不定,即C选项错误;
对于D选项,等价于
<
,即函数y=
在区间(-1,0)上递增,而y=
表示函数y=f(x)图象上任一点与坐标原点连线的斜率,由图象知其递增,即D选项正确.
故选:C.
对于B选项,导函数f′(x)即为y=f(x)图象上任一点处切线的斜率,递增,即B选项正确;
对于C选项,等价于x1-f(x1)≤x2-f(x2),而函数y=x-f(x)的导函数为y′=1-f′(x),其符号先正后负,即函数y=x-f(x)先增后减,故x1-f(x1)与x2-f(x2)的大小关系不定,即C选项错误;
对于D选项,等价于
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(x) |
| x |
| f(x) |
| x |
故选:C.
点评:本题考查了识图能力与函数单调性的判断,以及导数的几何意义,属中档题.分析四个选项,研究对应函数的性质,即得正解.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
如图所示的程序框图运行后,输出的S的值是( )


| A、6 | B、15 | C、31 | D、63 |
设α是一个平面,m,n是两条不同的直线,以下命题不正确的是( )
| A、若m∥α,n⊥α,则m⊥n |
| B、若m∥α,m⊥n,则n⊥α |
| C、若m⊥α,n⊥α,则m∥n |
| D、若m⊥α,m∥n,则n⊥α |
已知数列{an}为等差数列,且a3+a9=
,sina6cosa6的值为( )
| 4π |
| 3 |
A、-
| ||||
B、
| ||||
C、±
| ||||
D、-
|
已知向量
,
满足|
+
|=|
-
|=2|
|=2,则|
+2
|等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、2
| ||
B、
| ||
| C、3 | ||
| D、4 |
设a>b>0,a+b=1且x=(
)b,y=log (
+
)a,z=log
a,则x,y,z的大小关系是( )
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| A、y<x<z |
| B、z<y<x |
| C、y<z<x |
| D、x<y<z |
设全集U={x∈N|x≤5},A={0,1,2,3},B={0,3,4,5},则B∩(∁UA)=( )
| A、{3} |
| B、{4,5} |
| C、{3,4,5} |
| D、{4,5,6} |