题目内容
7.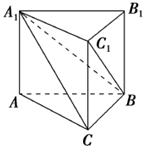 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.(Ⅰ)求证:四棱锥B-A1ACC1为阳马;并判断四面体B-A1CC1是否为鳖臑,若是,请写出各个面的直角(只要求写出结论).
(Ⅱ)若A1A=AB=2,当阳马B-A1ACC1体积最大时,求二面角C-A1B-C1的余弦值.
分析 (Ⅰ)由堑堵ABC-A1B1C1的性质得:四边形A1ACC1是矩形,推导出BC⊥A1A,BC⊥AC,从而BC⊥平面A1ACC1,由此能证明四棱锥B-A1ACC1为阳马,四面体B-A1CC1是否为鳖臑,四个面的直角分别是∠A1CB,∠A1C1C,∠BCC1,∠A1C1B.
(Ⅱ)阳马B-A1ACC1的体积:$V=\frac{1}{3}{S}_{矩形{A}_{1}AC{C}_{1}}•BC$≤$\frac{1}{3}(A{C}^{2}+B{C}^{2})=\frac{1}{3}×A{B}^{2}=\frac{4}{3}$,当且仅当AC=BC=$\sqrt{2}$时,${V}_{max}=\frac{4}{3}$,以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出当阳马B-A1ACC1体积最大时,二面角C-A1B-C1的余弦值.
解答 证明:(Ⅰ)由堑堵ABC-A1B1C1的性质得:四边形A1ACC1是矩形,
∵A1A⊥底面ABC,BC?平面ABC,
∴BC⊥A1A,又BC⊥AC,A1A∩AC=A,A1A,AC?平面A1ACC1,
∴BC⊥平面A1ACC1,
∴四棱锥B-A1ACC1为阳马,
四面体B-A1CC1是否为鳖臑,四个面的直角分别是∠A1CB,∠A1C1C,∠BCC1,∠A1C1B.
解:(Ⅱ)∵A1A=AB=2,
由(Ⅰ)知阳马B-A1ACC1的体积:
$V=\frac{1}{3}{S}_{矩形{A}_{1}AC{C}_{1}}•BC$=$\frac{1}{3}×{A}_{1}A×AC×BC$=$\frac{2}{3}AC×BC$≤$\frac{1}{3}(A{C}^{2}+B{C}^{2})=\frac{1}{3}×A{B}^{2}=\frac{4}{3}$,
当且仅当AC=BC=$\sqrt{2}$时,${V}_{max}=\frac{4}{3}$,
以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,
则A1(0,$\sqrt{2}$,2),B($\sqrt{2}$,0,0),C1(0,0,2),
∴$\overrightarrow{C{A}_{1}}$=(0,$\sqrt{2}$,2),$\overrightarrow{CB}$=($\sqrt{2}$,0,0),$\overrightarrow{{C}_{1}{A}_{1}}$=(0,$\sqrt{2}$,0),$\overrightarrow{{C}_{1}B}$=($\sqrt{2}$,0,-2),
设平面CA1B的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{C{A}_{1}}=\sqrt{2}y+2z-0}\\{\overrightarrow{n}•\overrightarrow{CB}=\sqrt{2}x=0}\end{array}\right.$,取y=$\sqrt{2}$,得$\overrightarrow{n}$=(0,$\sqrt{2}$,-1),
设平面C1A1B的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{{C}_{1}{A}_{1}}=\sqrt{2}b=0}\\{\overrightarrow{m}•\overrightarrow{{C}_{1}B}=\sqrt{2}a-2c=0}\end{array}\right.$,取a=$\sqrt{2}$,得$\overrightarrow{m}$=($\sqrt{2}$,0,1),
设当阳马B-A1ACC1体积最大时,二面角C-A1B-C1的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{3}•\sqrt{3}}$=$\frac{1}{3}$,
∴当阳马B-A1ACC1体积最大时,二面角C-A1B-C1的余弦值为$\frac{1}{3}$.
点评 本题考查四棱锥是阳马的证明,考查二面角的余弦值的求法,考查满足条件的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

 阅读快车系列答案
阅读快车系列答案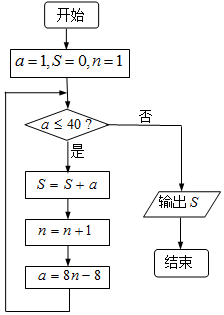 《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问题的程序框图,若设每层外周枚数为a,则输出的结果为( )
| A. | 81 | B. | 74 | C. | 121 | D. | 169 |
| A. | (-∞,0] | B. | (-∞,0]∪{$\frac{2}{e}$} | C. | (-∞,$\frac{2}{e}$) | D. | (-∞,$\frac{2}{e}$) |
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | 4 |
 与圆
与圆 的公共弦长为( )
的公共弦长为( ) B.
B. C.2
C.2 D.2
D.2