题目内容
17.已知点A(2,0),B(3,2),向量$\overrightarrow a=({2,λ})$,若$\overrightarrow a⊥\overrightarrow{AB}$,则$|{\overrightarrow a}|$为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | 4 |
分析 根据向量的数量积求出λ的值,再求其模即可.
解答 解:$\overrightarrow a\;•\;\overrightarrow{AB}=(2,\;\;λ)\;•\;(1,\;\;2)=2+2λ=0⇒λ=-1$,
$|\overrightarrow a|=\sqrt{{2^2}+{λ^2}}=\sqrt{5}$,
故选A.
点评 本题考查了向量的数量积公式和向量的垂直以及向量的模,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.复数$\frac{2i}{1-i}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.已知焦点为F的抛物线y2=2px(p>0)上有一点$A({m,2\sqrt{2}})$,以A为圆心,|AF|为半径的圆被y轴截得的弦长为$2\sqrt{7}$,则m=( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
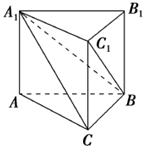 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC. 根据如图所示的伪代码,如果输出y=5,那么输入的x的组成的集合为{-5,5}.
根据如图所示的伪代码,如果输出y=5,那么输入的x的组成的集合为{-5,5}.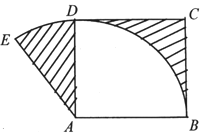 如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.
如图,以正方形ABCD中的点A为圆心,边长AB为半径作扇形EAB,若图中两块阴影部分的面积相等,则∠EAD的弧度数大小为2-$\frac{π}{2}$.