题目内容
2.若复数z满足(1+i)z=2i,其中i为虚数单位,则$\overline z$( )| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
分析 通过化简求出z,从而求出z的共轭复数即可.
解答 解:∵(1+i)z=2i,
∴z=$\frac{2i}{1+i}$=i(1-i)=1+i,
则$\overline z$=1-i,
故选:A.
点评 本题考查了复数的运算,考查复数的化简求值,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.设$a={log_5}4,b={log_{\sqrt{2}}}3,c={({{{log}_{0.2}}3})^2}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | b>c>a | C. | a>c>b | D. | b>a>c |
11.正项等比数列{an}中,存在两项am、an使得$\sqrt{{a_m}•{a_n}}=2{a_1}$,且a6=a5+2a4,则$\frac{1}{m}+\frac{4}{n}$的最小值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{9}{4}$ |
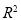 的值判断的拟合效果,
的值判断的拟合效果,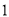 ;
;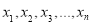 的方差为
的方差为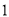 ,则
,则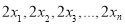 的方差为
的方差为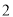 ;
;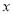 与
与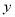 的随机变量
的随机变量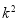 的观测值
的观测值 来说,
来说, 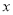 与
与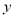 有关系”的把握程度越大.
有关系”的把握程度越大.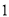 B.
B.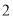 C.
C.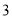 D.
D.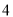
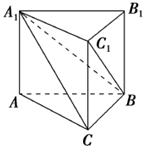 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.