题目内容
15.已知函数f(x)=a+$\sqrt{x}$lnx在(0,+∞)上有且仅有1个零点,则实数a的取值范围为( )| A. | (-∞,0] | B. | (-∞,0]∪{$\frac{2}{e}$} | C. | (-∞,$\frac{2}{e}$) | D. | (-∞,$\frac{2}{e}$) |
分析 问题转化为y=-a和g(x)=$\sqrt{x}$lnx在(0,+∞)只有1个交点,根据函数的单调性判断即可.
解答 解:函数f(x)=a+$\sqrt{x}$lnx在(0,+∞)上有且仅有1个零点,
即y=-a和g(x)=$\sqrt{x}$lnx在(0,+∞)只有1个交点,
g′(x)=$\frac{1}{2\sqrt{x}}$lnx+$\frac{1}{\sqrt{x}}$=$\frac{1}{\sqrt{x}}$($\frac{1}{2}$lnx+1),
令g′(x)>0,解得:x>e-2,令g′(x)<0,解得:0<x<e-2,
故g(x)在(0,e-2)递减,在(e-2,+∞)递增,
故g(x)min=g(e-2)=-$\frac{2}{e}$,
在(0,e-2)时,g(x)<0,在x≥1时,g(x)≥0,
故-a=-$\frac{2}{e}$即a=$\frac{2}{e}$时,1个交点,-a≥0即a≤0时,1个交点,
故选:B.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数的零点问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.执行如下图所示的程序框图,输出S的值为( )


| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为________
的最大值为________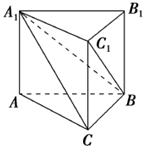 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.
《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC-A1B1C1中,AC⊥BC.