题目内容

6．（1+x）3+（1+x）4+…+（1+x）50的展开式中的x3的系数为47600．

分析 分别写出每一项中含x3项的系数，作和后利用组合数公式的性质求得结果．

解答 解：（1+x）3+（1+x）4+…+（1+x）50的展开式中的x3的系数为C33+C43+C53+…+C503=C44+C43+C53+…+C503=C514=47600，
故答案为：47600

点评 本题主要考查二项式定理的应用，求展开式中某项的系数，考查组合数公式的性质，属于中档题．

练习册系列答案
相关题目
16．已知函数f（x）是定义在R上的偶函数，若任意的x≥0，都有f（x+2）=-f（x），当x∈[0，1]时，f（x）=2x-1，则f（-2017）+f（2018）=（　　）
A．1B．-1C．0D．2
17．下列函数是偶函数的是（　　）
A．y=tan3xB．y=cos2x+1C．y=2sinx-1D．y=2x
14．已知各项为正数的数列{an}，满足$\frac{1}{{{a_{n+1}}}}=\frac{1}{{{a_n}+1}}$，n∈N*，其中a1=1，Sn为其前n项的和．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列$\left\{{\left.{\frac{1}{S_n}}\right\}}\right.$的前n项和Tn．
1．设数列{an}满足an+1=an2-nan+1，n=1，2，3，…．
（1）当a1=2时，求a2，a3，a4，并由此猜想出{an}的一个通项公式；
（2）当a1≥3时，用数学归纳法证明对所有n≥1，有an≥n+2．
11．已知向量$|{\overrightarrow a}|=3，|{\overrightarrow b}|=2$，且$\overrightarrow a，\overrightarrow b$的夹角为120°，求：
（1）求$（{2\overrightarrow a+\overrightarrow b}）•（{\overrightarrow a-2\overrightarrow b}）$的值；
（2）求$|{2\overrightarrow a+\overrightarrow b}|$的值．
18．已知$f（x）=a{sin^3}x+b\root{3}{x}{cos^3}x+4（a，b∈R），且f（sin10°）=5$，则f（cos100°）=3．
15．设a=log32，b=ln2，$c={5^{\frac{1}{2}}}$则（　　）
A．c＞b＞aB．a＞b＞cC．a＞c＞bD．b＞a＞c
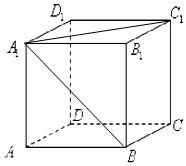16．如图，正方体ABCD-A1B1C1D1棱长为1．
（1）求证：BD1⊥平面ACB1；
（2）求直线BA1与平面A1C1D1所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网