题目内容
17．下列函数是偶函数的是（ ）| A． | y=tan3x | B． | y=cos2x+1 | C． | y=2sinx-1 | D． | y=2x |
分析 利用函数奇偶性的定义逐个判断．
解答 解：∵tan（-3x）=-tan3x，∴y=tan3x是奇函数；
∵cos（-2x）+1=cos2x+1，∴y=cos2x+1是偶函数；
∵2sin（-x）-1=-2sinx-1，∴y=2sinx-1为非奇非偶函数；
∵2-x=$\frac{1}{{2}^{x}}$，∴y=2x为非奇非偶函数．
故选B．
点评 本题考查了函数奇偶性的判断，属于基础题．
练习册系列答案
相关题目
7．数列{an}满足a1=2，an+1=$\frac{2（n+2）}{n+1}$an（n∈N*），$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=（ ）
| A． | $\frac{1009}{1008}$ | B． | $\frac{2015}{1007}$ | C． | $\frac{2016}{2015}$ | D． | $\frac{2015}{2014}$ |
5．已知集合A={x||x-1|＜1}，B={x|x2-1＜0}，则A∪B=（ ）
| A． | （-1，1） | B． | （-1，2） | C． | （1，2） | D． | （0，1） |
12．设D为△ABC中BC边上的中点，且O为AD边的中点，则（ ）
| A． | $\overrightarrow{BO}=-\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$ | B． | $\overrightarrow{BO}=-\frac{1}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$ | C． | $\overrightarrow{BO}=\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$ | D． | $\overrightarrow{BO}=-\frac{1}{2}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$ |
2．
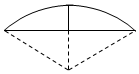《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积=$\frac{1}{2}×$（弦×矢+矢2），弧田（如图）由圆弧和其所对弦围城，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角$\frac{2π}{3}$，半径为6米的弧田，按照上述经验公式计算所得弧田面积约是（$\sqrt{3}≈1.73$）（ ）
《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积=$\frac{1}{2}×$（弦×矢+矢2），弧田（如图）由圆弧和其所对弦围城，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角$\frac{2π}{3}$，半径为6米的弧田，按照上述经验公式计算所得弧田面积约是（$\sqrt{3}≈1.73$）（ ）| A． | 16平方米 | B． | 18平方米 | C． | 20平方米 | D． | 25平方米 |
9．
把正整数按“f（x）”型排成了如图所示的三角形数表，第f（x）行有f（x）个数，对于第f（x）行按从左往右的顺序依次标记第1列，第2列，…，第f（x）列（比如三角形数表中12在第5行第4列，18在第6行第3列），则三角形数表中2017在（ ）
把正整数按“f（x）”型排成了如图所示的三角形数表，第f（x）行有f（x）个数，对于第f（x）行按从左往右的顺序依次标记第1列，第2列，…，第f（x）列（比如三角形数表中12在第5行第4列，18在第6行第3列），则三角形数表中2017在（ ）| A． | 第62行第2列 | B． | 第64行第64列 | C． | 第63行第2列 | D． | 第64行第1列 |
