题目内容
如果圆(x-a)2+(y-a)2=2上有且只有两个点到原点的距离为1,则正实数a的取值范围是 .
考点:圆的标准方程
专题:计算题,直线与圆
分析:根据题意知:圆(x-a)2+(y-a)2=2和以原点为圆心,1为半径的圆x2+y2=1相交,因此两圆圆心距大于两圆半径之差、小于两圆半径之和,列出不等式,解此不等式即可.
解答:
解:圆(x-a)2+(y-a)2=2和圆x2+y2=1相交,两圆圆心距d=
|a|,
∴
-1<
|a|<
+1,
∵a>0,
∴0<a<2-
.
故答案为:0<a<2-
.
| 2 |
∴
| 2 |
| 2 |
| 2 |
∵a>0,
∴0<a<2-
| 2 |
故答案为:0<a<2-
| 2 |
点评:本题体现了转化的数学思想,解题的关键在于将问题转化为:圆(x-a)2+(y-a)2=2和圆x2+y2=1相交,属中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
在直三棱柱ABC-A1B1C1中,若
=
,
=
,
=
,则
等于( )
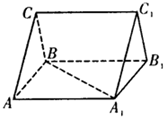
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |

A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|