题目内容
4.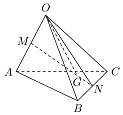 如图,空间四边形OABC中,M、N分别是对边OA、BC的中点,点G在线段MN上,分$\overrightarrow{MN}$所成的定比为2,$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$.
如图,空间四边形OABC中,M、N分别是对边OA、BC的中点,点G在线段MN上,分$\overrightarrow{MN}$所成的定比为2,$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$.
分析 根据$\overrightarrow{OG}$=$\overrightarrow{OM}+\overrightarrow{MG}$,$\overrightarrow{OM}$=$\frac{1}{2}\overrightarrow{OA}$,$\overrightarrow{MG}$=$\frac{2}{3}\overrightarrow{MN}$,$\overrightarrow{MN}$=$\overrightarrow{ON}-\overrightarrow{OM}$,$\overrightarrow{ON}$=$\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$,代入计算即可得出.
解答 解:∵$\overrightarrow{OG}$=$\overrightarrow{OM}+\overrightarrow{MG}$,$\overrightarrow{OM}$=$\frac{1}{2}\overrightarrow{OA}$,$\overrightarrow{MG}$=$\frac{2}{3}\overrightarrow{MN}$,
$\overrightarrow{MN}$=$\overrightarrow{ON}-\overrightarrow{OM}$,$\overrightarrow{ON}$=$\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$,
∴$\overrightarrow{OG}$=$\frac{1}{6}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$.
∴$x=\frac{1}{6}$,$y=z=\frac{1}{3}$.
故答案为:$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$.
点评 本题考查了向量平行四边形法则、向量共线定理、空间向量基本定理,考查了推理能力与计算能力,属于基础题.

 名校课堂系列答案
名校课堂系列答案| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
| A. | 外接球的体积为12$\sqrt{3}$ π | B. | 外接球的表面积为4π | ||
| C. | 体积为$\sqrt{2}$ | D. | 表面积为$\sqrt{5}$+$\sqrt{2}$+1 |
 执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )
执行如图所示的程序框图,如果输入的m=15,n=12,则输出的n是( )| A. | 15 | B. | 12 | C. | 3 | D. | 180 |
| A. | $\frac{15}{16}$ | B. | $\frac{3}{16}$ | C. | $\frac{15}{2}$ | D. | $\frac{15}{4}$ |
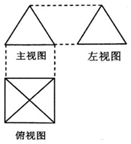 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.