题目内容
13.斜率为1的直线l过椭圆$\frac{{x}^{2}}{4}$+y2=1的右焦点,交椭圆与AB两点,求弦长AB,及三角形OAB的面积.分析 由题意方程求出椭圆的右焦点坐标,写出直线l的方程,和椭圆方程联立,化为关于x的一元二次方程,利用弦长公式求得弦长,再由点到直线的距离公式求出坐标原点到直线l的距离,代入三角形面积公式得答案.
解答 解:由$\frac{{x}^{2}}{4}$+y2=1,得a2=4,b2=1,
∴c2=a2-b2=3,则c=$\sqrt{3}$.
∴椭圆的右焦点F($\sqrt{3},0$),
则直线l的方程为y=x-$\sqrt{3}$.
联立$\left\{\begin{array}{l}{y=x-\sqrt{3}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$5{x}^{2}-8\sqrt{3}x+8=0$.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{8\sqrt{3}}{5},{x}_{1}{x}_{2}=\frac{8}{5}$.
∴$|AB|=\sqrt{2}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}•\sqrt{(\frac{8\sqrt{3}}{5})^{2}-\frac{32}{5}}=\frac{8}{5}$;
O到直线AB的距离为d=$\frac{|-\sqrt{3}|}{\sqrt{2}}=\frac{\sqrt{6}}{2}$.
∴${S}_{△OAB}=\frac{1}{2}|AB|•d=\frac{1}{2}×\frac{8}{5}×\frac{\sqrt{6}}{2}=\frac{2\sqrt{6}}{5}$.
点评 本题考查椭圆的简单性质,考查了直线和椭圆的位置关系的应用,是中档题.

 优加精卷系列答案
优加精卷系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分与不必要条件 |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| 区间界限 | [122,126) | [126,130) | [130,134) | [134,138) | [138,142) |
| 人数 | 5 | 8 | 10 | 22 | 33 |
| 区间界限 | [142,146) | [146,150) | [150,154) | [154,158) | |
| 人数 | 20 | 11 | 6 | 5 |
(2)画出频率分布直方图;
(3)估计身高低于134厘米的人数占总人数的百分比和身高在区间[134,146)(厘米)内的人数占总人数的百分比.
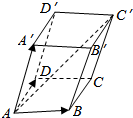 在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.
在平行六面体(底面是平行四边形的四棱柱)ABCD-A′B′C′D′中,分别标出$\overrightarrow{AB}$+$\overrightarrow{AD}$+$\overrightarrow{AA′}$,$\overrightarrow{AB}$+$\overrightarrow{AA′}$+$\overrightarrow{AD}$表示的向量.从中你能体会向量加法运算的交换律及结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系.