题目内容
已知点P是双曲线
-
=1(a>0,b>0)的渐近线上一点,F是双曲线的右焦点,若|PF|的最小值为
a,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:第一步:写出双曲线的渐近线方程,并化为一般式;
第二步:根据点到直线的距离公式及|PF|的最小值列出a,b,c的等量关系,从而得到a,c的齐次关系式;
第三步:由e=
得双曲线的离心率.
第二步:根据点到直线的距离公式及|PF|的最小值列出a,b,c的等量关系,从而得到a,c的齐次关系式;
第三步:由e=
| c |
| a |
解答:
解:由双曲线的方程,得其渐近线方程为y=±
x,即bx±ay=0,
|PF|的最小值即为焦点F(c,0)到渐近线的距离,
由题意得
=
a,由a2+b2=c2,得a=2b,
∴a2=4b2=4(c2-a2),即5a2=4c2,
得双曲线的离心率e=
=
.
故选C.
| b |
| a |
|PF|的最小值即为焦点F(c,0)到渐近线的距离,
由题意得
| |bc| | ||
|
| 1 |
| 2 |
∴a2=4b2=4(c2-a2),即5a2=4c2,
得双曲线的离心率e=
| c |
| a |
| ||
| 2 |
故选C.
点评:本题考查了双曲线的离心率的求法,关键是根据题设条件得到关于a,c的齐次等式.值得注意的是,隐含条件a2+b2=c2可实现b与a,c之间的转化.

练习册系列答案
相关题目
复数
的实部与虚部之和为( )
| 2 |
| 1-i |
| A、-1 | B、2 | C、1 | D、0 |
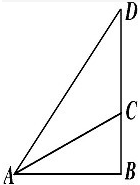 已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=
已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=