题目内容
已知实数m,n都为正数,且
+
=1,求m+n+
的最小值.
| 2 |
| m |
| 9 |
| n |
| m2+n2 |
考点:基本不等式
专题:不等式的解法及应用
分析:由题目提炼出其几何意义为求过点(2,9)的直线与两坐标轴正半轴相交所围成的三角形的周长的最小值,然后利用三角代换列出三角形的周长,然后借助于导数求得最小值.
解答:
解:原题的几何意义是求过点(2,9)的直线与两坐标轴正半轴相交所围成的三角形的周长的最小值.
设三角形三个顶点坐标分别为O(0,0),A(m,0),B(0,n),其中m>0,n>0,
如图
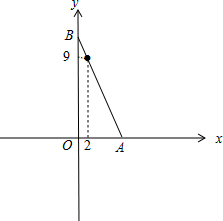
设角OAB=α,α∈(0,
),则:
OA=m=2+
,
OB=n=9+2tanα,
AB=
+
,
周长l=OA+AB+BO=11+
+2tanα+
+
=11+
.
令tan
=x,x∈(0,1),
则l=11+
=
=9+
=9+
.
令t=
,则t′=
,由t′=0得x=9±6
.
当x∈(0,9-6
),(9+6
,+∞)时,t′<0,当x∈(9-6
,9+6
),t′>0.
∴当x=9-6
时,l有最小值为26+12
.
设三角形三个顶点坐标分别为O(0,0),A(m,0),B(0,n),其中m>0,n>0,
如图
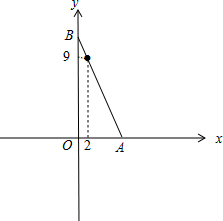
设角OAB=α,α∈(0,
| π |
| 2 |
OA=m=2+
| 9 |
| tanα |
OB=n=9+2tanα,
AB=
| 9 |
| sinα |
| 2 |
| cosα |
周长l=OA+AB+BO=11+
| 9 |
| tanα |
| 9 |
| sinα |
| 2 |
| cosα |
=11+
2tan3
| ||||||
tan
|
令tan
| α |
| 2 |
则l=11+
| 2x3-5x2+2x+9 |
| x-x3 |
| 9+13x-5x2-9x3 |
| x-x3 |
| -5x2+4x+9 |
| x-x3 |
| 9-x |
| x(1-x) |
令t=
| 9-x |
| x(1-x) |
| -x2+18x-9 |
| x2(1-x)2 |
| 2 |
当x∈(0,9-6
| 2 |
| 2 |
| 2 |
| 2 |
∴当x=9-6
| 2 |
| 2 |
点评:本题考查了直线与方程,考查了数学转化思想方法,考查了同角三角函数的基本关系式,训练了利用导数求函数的最值,是难度较大的题目.

练习册系列答案
相关题目
 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=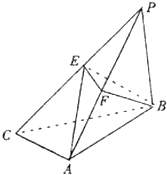 如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4
如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=BA=CA=4