题目内容
桌面上一矩形纸板ABCD，绕边AB旋转
，再绕边AD旋转
，则此时的平面与旋转前的平面所成的二面角的大小为 ．
| π |
| 4 |
| π |
| 4 |
考点：二面角的平面角及求法
专题：空间角
分析：首先根据旋转体问题，把空间问题平面化，进一步利用公式求解．
解答：
解：上一矩形纸板ABCD，绕边AB旋转θ=
，再绕边AD旋转α=
，
此时的平面与旋转前的平面所成的二面角的大小为β，
则最后利用公式：cosβ=cosθ•cosα，
则求得：β=
，
故答案为：
．
| π |
| 4 |
| π |
| 4 |
此时的平面与旋转前的平面所成的二面角的大小为β，
则最后利用公式：cosβ=cosθ•cosα，
则求得：β=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查的知识要点：二面角问题的转化，旋转体问题．属于中档题型．
练习册系列答案
相关题目
如图，在程序框图中，若输入n=3，则输出k的值是（ ）
| A、2 | B、3 | C、4 | D、5 |
已知集合A={x∈R|
＜2x＜8}，B={x∈R|-2＜x≤4}，则A∩B等于（ ）
| 1 |
| 2 |
| A、（-1，3） | ||
| B、（-1，4） | ||
C、(
| ||
D、(
|
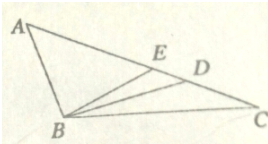在△ABC中，E为线段AC的中点，试问在线段AC上是否存在一点D．使得
如图，在四棱锥S-ABCD中，底面ABCD是正方形，且SA=SB=SC=SD，SO是这个三棱锥的高，SM垂直于BC，垂足为M，若SO=8，SM=10．