题目内容
设以
=(1,-2)为方向向量的直线的倾斜角为α,则sin(2α+
)=( )
. |
| e |
| π |
| 4 |
A、
| ||||
B、7
| ||||
C、
| ||||
D、-
|
考点:二倍角的正弦,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:由方向向量可得tanα=-2,可得sin2α和cos2α的值,再有两角和的正弦可得.
解答:
解:∵以
=(1,-2)为方向向量的直线的倾斜角为α,
∴tanα=-2,∴sin2α=2sinαcosα=
=
=-
,
∴cos2α=cos2α-sin2α=
=-
,
∴sin(2α+
)=
sin2α+
cos2α=
(sin2α+cos2α)=
×(-
)=-
故选:D.
. |
| e |
∴tanα=-2,∴sin2α=2sinαcosα=
| 2sinαcosα |
| sin2α+cos2α |
| 2tanα |
| 1+tan2α |
| 4 |
| 5 |
∴cos2α=cos2α-sin2α=
| cos2α-sin2α |
| sin2α+cos2α |
| 3 |
| 5 |
∴sin(2α+
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 7 |
| 5 |
7
| ||
| 10 |
故选:D.
点评:本题考查三角函数的公式的综合应用,涉及直线的方向向量,属中档题.

练习册系列答案
相关题目
设全集U=R,函数y=lg(2-x)的定义域为A,集合B={x|1<x<3},则(∁UA)∩B等于( )
| A、[2,3) |
| B、(1,2) |
| C、(2,3) |
| D、[1,2) |
若sin(
-θ)=
,则cos(
+2θ)的值为( )
| π |
| 6 |
| 1 |
| 3 |
| 2π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知角α的始边为x轴正半轴,终边上有一点P(m,n)(n≠0)若α=-420°,则
的值为( )
| n |
| m |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若框图所给的程序运行结果为V=10,那么判断框中可以填入的关于n的条件是( )


| A、n<19? |
| B、n≤19? |
| C、n<18? |
| D、n≤18? |
从10张分别标有数字1,2,3,4,5,6,7,8,9,10的卡片中抽取4张卡片,则这4卡片上数字从小到大成等差数列的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
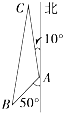 我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )
我舰在敌岛A处南偏西50°的B处,且AB距离为12海里,发现敌舰正离开岛沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )| A、28海里/小时 | ||
| B、14海里/小时 | ||
C、14
| ||
| D、20海里/小时 |